7.5 – Odds ratio

Introduction
Example
Odds ratio interpretation
Relative risk v. odds ratio
Hazard ratio
Questions
Chapter 7 contents

Introduction

We introduced the concept of odds 7.1 — Epidemiology definitions. As a reminder, odds are a way to communicate the chance (likelihood) that a particular event will take place. Odds are calculates as the number of individuals with the event divided by the number of individuals without the event.

Odds ratio definition: is a measure of effect size for the association between two binary (yes/no) variables. It is the ratio of the odds of an event occurring in one group to the odds of the same event happening in another group. The odds ratio (OR) is a way to quantify the strength of association between one condition and another.

Note: Effect size — the size of the difference between groups — is discussed further in Chapter 9.2 and Chapter 11.4.

How are odds ratios calculated? The probabilities are conditional; recall that conditional probability of some event A, given the occurrence of some other event B.

Let $p_{y-y}$ equal probability of the event occurring (y = Yes) in A, $p_{y-n}$ equal probability of the event not occurring (n = No) in A, $p_{n-y}$ equal probability of the event occurring in B, and $p_{n-n}$ equal probability of the event not occurring in B.

		A
		Yes	No
B	Yes	$p_{y-y}$	$p_{y-n}$
B	No	$p_{n-y}$	$p_{n-n}$

These sum to one: $p_{y-y}+p_{y-n}+p_{n-y}+p_{n-n} = 1$

The conditional probabilities are

		A
		Yes	No
B	Yes	$\frac{p_{y-y}}{\left ( p_{y-y}+p_{y-n} \right )}$	$\frac{p_{y-n}}{\left ( p_{y-y}+p_{y-n} \right )}$
B	No	$\frac{p_{n-y}}{\left ( p_{n-y}+p_{n-n} \right )}$	$\frac{p_{n-n}}{\left ( p_{n-y}+p_{n-n} \right )}$

and finally then, the odds ratio (OR) is

$\begin{align*} OR = \frac{p_{y-y} \cdot p_{n-n}}{p_{y-n} \cdot p_{n-y}} \end{align*}$

If you have the raw numbers you can calculate the odds ratio directly, too.

		A
		Yes	No
B	Yes	a	b
B	No	c	d

and the odds ratio is then

$\begin{align*} OR = \frac{a \div b}{c \div d} \end{align*}$

or, equivalently

$\begin{align*} OR = \frac{a \cdot d}{b \cdot c} \end{align*}$

Example

Comparing proportions is a frequent need in court. Gray (2002) provided an example from Title IX of the Education Act of 1972 case Cohen v. Brown University. Under the Act, discrimination based on gender is prohibited. The case concerned participation in collegiate athletics by women. The case data were that of the 5722 undergraduate students, 51% were women, but of the 987 athletes, only 38% were women. A mosaic plot shows graphically these proportions (Fig. 1, males in red bars, females in yellow bars).

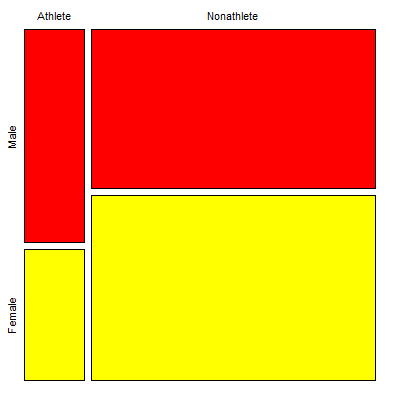
Mosaic plot of athletes to non-athletes in college. Males red, females yellow, data from Gray 2002.

Figure 1. Mosaic plot of athletes to non-athletes in college. Males red, females yellow, data from Gray 2002.

Alternatively, use a Venn diagram to describe the distribution (Fig. 2). Circles that overlap show regions of commonality.

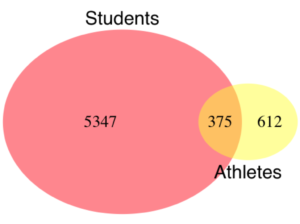
Venn diagram

Figure 2. Venn Diagram of athletes to non-athletes in college. Female athletes (n = 375), male athletes (n = 612), data from Gray 2002.

where the orange region

$\begin{align*} Students \cap Female Athletes \end{align*}$

R code for the Venn diagram was

library(VennDiagram)
area1 = 5722
area2 = 987 
cross.area = 375 
draw.pairwise.venn(area1,area2,cross.area,category=c("Students","Athletes"),
euler.d = TRUE, scaled = TRUE, inverted = FALSE, print.mode = "percent",
fill=c("Red","Yellow"),cex = 1.5, lty="blank", cat.fontfamily = rep("sans", 2),
cat.cex = 1.7, cat.pos = c(0, 180), ext.pos=0)

The question raised before the court was whether these proportions meet the demand of “substantially proportionate.” What exactly the law means by “substantially proportionate” was left to the courts and the lawyers to work out (Gray 2002). Title IX suggests that “substantially proportionate” is a statistical problem and the two sides of the argument must address the question from that perspective.

What is the chance that an undergraduate student was an athlete and female? 38% And the chance that an undergraduate student was an athlete and male? 62% Clearly 38% is not 62%; did the plaintiffs have a case?

Graphs like Figure 1 and Figure 2 help communicate but can’t provide a sense of whether the differences are important. Let’s start by looking at the numbers. Working with the proportions we have the following break down for numbers of students (Table 1) or as proportions (Table 2).

Table 1. Gray’s raw data displayed in a 2 x 2 format.

		Athletes
		Yes	No
Undergraduates	Male	612	2192
Undergraduates	Female	375	2543

Together, the numbers total 5,722.

The Odds Ratio (OR) would be

$\begin{align*} OR = \frac{612 \cdot 2543}{2192 \cdot 375} = 1.89 \end{align*}$

Or from the proportions (Table 2)

Table 2. Data from Table 1 as proportions.

		Athletes
		Yes	No
Undergraduates	Male	0.107	0.383
Undergraduates	Female	0.066	0.444

adding all of these frequencies together equal 1. Carry out the calculation of odds (Table 3), the conditional probabilities (in bold).

Table 3. Odds calculated from Table 2 inputs.

		Athletes
		Yes	No
Undergraduates	Male	0.218 $= \frac{0.107}{\left ( 0.107+0.383\right )}$	0.782 $= \frac{0.383}{\left ( 0.107+0.383\right )}$
Undergraduates	Female	0.129 $= \frac{0.066}{\left ( 0.066+0.444\right )}$	0.871 $= \frac{0.444}{\left ( 0.066+0.444\right )}$

Calculate the odds ratio

$\begin{align*} OR = \frac{0.2182 \cdot 0.871}{0.129 \cdot 0.782} = 1.89 \end{align*}$

Thankfully, whether we use the raw number format or the proportion format, we got the same results!

Odds ratio interpretation

Because the Odds Ratio (OR) was greater than 1, males students were more likely to be athletes than female students. If there was no difference in proportion of male and female athletes, the odds ratio would be close to one. That is a test of statistical inference (e.g., a contingency table), but for now, if one is included in the confidence interval, then this would be evidence that there was no difference between the proportions.

And in R? Simple enough, just create a matrix then apply the Fisher test. which we will discuss further in Chapter 9.5.

title9 <- matrix(c(612, 2192, 375, 2543), nrow=2))
fisher.test(title9)

and results

p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.641245 2.185576
sample estimates:
odds ratio 
1.893143

Thankfully, they agree. But note, we now have confidence intervals and a p-value, which we use to conduct inference: were the odds “significantly different from 1?” We would conclude, yes! Between the lower limit (1.64) and the upper limit (2.19), the value “1” was excluded. Moreover, the p-value at 2.2e-16 was much less than the standard type I error cut-off of 5% (see Chapter 8).

Before we leave the interpretation, sometimes a calculated odds-ratio is less than one. If our calculated odds ratio for the Title IX case described in Table 1 was less than 1, (say, the numbers were flipped, Table 4) we then the interpretation would be females were more likely to be athletes on college campus.

Table 4. Table 1 data, but order of entry changed.

		Athletes
		Yes	No
Undergraduates	Female	375	2543
Undergraduates	Male	612	2192

Now, calculating the odds via Fisher exact test, the odds ratio is less than one (0.53):

Fisher's Exact Test for Count Data
p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.4575452 0.6092936
sample estimates:
odds ratio 
0.5282222

Note this result is for the same data (Table 1 vs Table 4), just the order by which the groups are specified changed. Of course they are related to each other mathematically, and in a simple way. Note that taking the inverse (reciprocal) odds ratio.

$\begin{align*} OR = \frac{1}{0.5282222} = 1.89 \end{align*}$

will return the comparison we wanted in the first place — the odds a student athlete was male. As long as you keep track of the comparison, of the groups, it may be easier to communicate results when the reported odds ratio is greater than one.

Relative risk v. odds ratio

We introduced another way to quantify this association as the Relative Risk (RR) and Absolute Risk Reductions in the previous section. Both can be used to describe the risk of the treatment (exposed) group relative to the control (nonexposed) group. RR is the ratio the treated to control group. OR is the ratio between odds of treated (exposed) and control (nonexposed). What’s the difference? OR is more general — it can be used in situations in which the researcher choses the number of affected individuals in the groups and, therefore, the base rate or prevalence of the condition in the population is not known or is not representative of the population, whereas RR is appropriate when prevalence is known (this is a general point, but see Schechtman 2002 for a nice discussion).

The odds ratio is related to relative risk, but not over the entire range of possible risk. Odds of an event is simply the number of individuals with the event divided by the number without the event. Odds of an event therefore can range from zero (event cannot occur) to infinity (event must occur). For example, odds of eight (1.89:1) means that nearly two male students were student athletes at Brown University for every one female student.

In contrast, the risk of an event occurring is the number of individuals with the event divided by the total number of people at risk of having that event. Risk is expressed as a percentage (Davies et al 1998). Thus, for our example, odds of 1.89:1 correspond to a risk of 1.89 divided by (1 + 1.89) equals 65%.

To get the relative risk we can use

$\begin{align*} RR = \frac{\frac{a}{a+b}}{\frac{c}{c+d}} \end{align*}$

or 1.7% for our example.

In this example we could use either odds or relative risk; the key distinction is that we knew how many events happened in both groups. If this information is missing for one group (e.g., control group of the case-control design), then only the odds ratio would be appropriate.

From cumulative wisdom in the literature (e.g., Tamhane et al 2107), if prevalence is less than ten percent, OR ≈ RR. We can relate RR and OR as

$\begin{align*} RR=OR\cdot \frac{1+\frac{n_{21}}{n_{22}}}{1+\frac{n_{11}}{n_{12}}} \end{align*}$

where n₁₁ and n₂₁ are the frequency with the condition for group 1 and group 2, respectively, and n₁₂ and n₂₂ are the frequency without the condition for group 1 and group 2, respectively. For the examples on this page group 1 is the treatment group and group 2 is the control group.

Hazard ratio

The hazard ratio is the ratio of hazard rates. Hazard rates are like the relative risk rates, but are specific to a period of time. Hazard rates come from a technique called Survival Analysis (introduced in Chapter 20.9). Survival analysis can be thought of as following a group of subjects over time until something (the event) happens. By following two groups, perhaps one group exposed to a suspected carcinogen vs. another group matched in other respects except the exposure, at the end of the trial, we’ll have two hazard rates: the rate for the exposed group and the rate for the control group. If there is no difference, then the hazard ratio will be one.

Hazard ratios are more appropriate for clinical trials; relative risk is more appropriate for observational studies.

For a hazard ratio, it is often easier to think of it as a probability (between 0 to 1). To translate a hazard ratio to a probability use the following equation

$\begin{align*} p =\frac{hazard \ ratio}{1+hazard \ ratio} \end{align*}$

Questions

Distinguish between odds ratio, relative risk, and hazard ratio.
Refer to problem 1 introduced in 7.4 – Epidemiology: Relative risk and absolute risk, explained
In 2017-18, males were 43% of the 18.8 million enrolled students at U.S. 2- and 4-year colleges, and 56% of the 4.95 million student athletes at that time. Calculate the odds, and confidence interval, that a student athlete was male in 2017-18. How do your results compare to the OR of 1.89 for Table 1 (from Gray 2002)?