7.6 – Confidence intervals

Introduction

Although I’ve already presented the concept (e.g., Chapter 3.4), and equations for confidence intervals of risk estimates (Chapter 7.4, Chapter 7.5), we’ll expand on the idea of confidence intervals. Confidence intervals are a central part of meeting one of the main objectives of statistics, that is, estimation. We will review how to calculate confidence intervals for proportions and for NNT. These intervals are available in epiR package and automatically returned in RcmdrPlugin.EBM.

There are three components of statistical analysis

  1. Estimation
  2. Inference
  3. Modeling

Inference refers to statistical hypothesis testing — we ask questions of observations — do men (Rice et al 1999) and women (Fisher et al 2012) differ for blood glucose levels following a bout of aerobic exercise? T-tests, analysis of variance (ANOVA), chi-square, correlation, regression are types of statistical procedures used to do statistical inference. Modeling on the other hand refers to procedures used to relate cause and effect. Many of the statistical procedures one uses for inference are also used to build statistical models (ANOVA, regression). Studies may intend to either test some hypothesis (inference) or to provide a predictive equation (modeling). But most studies that relate observations gathered from an experiment are obliged to also report statistics, and this is the realm of estimation. Estimates of the mean and standard deviation, for example, would be typical statistics one expects to find in a report. We call these descriptive statistics, and together with graphics, descriptive statistics are the chief way we describe our results.

Confidence interval for proportions

A proportion is the fraction of individuals in a population with some characteristic. The characteristic might be HIV positive for example. This would be called the population proportion and it would be a parameter of interest. In reality, we calculate a sample proportion and therefore estimate the population proportion with error. We can calculate the confidence interval (CI) of the proportion to communicate the precision of our estimate. For proportions, we use the binomial distribution — either a sample has the characteristic of interest or it does not — there are only two possibilities. There are a variety of ways to go here, and the simplest is to use a normal approximation. This will work well provided the sample size was reasonably large and the proportion is not close to zero or one, that is, we invoke the Central Limit Theorem here. Although the outcomes are binomial, the error is assumed to be normally distributed. The Wald confidence interval for p is

    \begin{align*} \% 95 \ CI = \hat{p} \pm z\sqrt{\frac{1}{n}\cdot \hat{p}\left ( 1- \hat{p} \right )} \end{align*}

where \hat{p} is the proportion of individuals with the characteristic (also called successes), z is the percentile from the normal distribution that corresponds to 1 – 1/2α.  For 95% CI then α = 0.05 and z would be 1.965. (See standard normal table.) Of course, if making the normal approximation for the binomial is not appropriate, the CI is less than ideal. The binomial after all is a discrete distribution whereas the normal distribution is continuous, so errors will enter particularly for low sample numbers.

Other approaches may be used to get better estimates of CI for proportions, including Wilson score intervals and Jeffrey Intervals (Agresti and Coull 1998). See R package propCIs.

Because a statistic like the mean or a calculation of absolute or relative risk reduction are calculated from samples drawn from a population, the estimate comes with error. The error is basically this – if we calculate a statistic like number needed to treat (NNT) or its converse, the number needed to harm (NNH), we need to communicate to the reader how precise our estimate is. Estimation has to do with accuracy, error, and precision.

Confidence interval for ARR

The ARR is simply \frac{c}{n_{2}}-\frac{a}{n_{1}}

where n_{1} is the number of treated or exposed individuals for which the event occurred and n_{2} is the number of untreated or unexposed individuals which the event occurred.

Event happened Event did not happen
Treated or
Exposed		 a b
Control or
Not exposed		 c d

Our data from example (Ch 7.5), were a = 612, b = 2192, c = 375, and d = 2543.

    \begin{align*} SE_{ARR}=\sqrt{\left (\frac{a}{n_{1}} \cdot \frac{1-\frac{a}{n_{1}}}{n_{1}} \right )+\left (\frac{c}{n_{2}} \cdot \frac{1-\frac{c}{n_{2}}}{n_{2}} \right )} \end{align*}

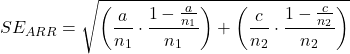
and the 95% confidence interval is then ARR \pm 2 \cdot SE_{ARR}

approximately. The “2” is only approximate; you need to use Z = 1.965, the value at probability value = 0.9725 (which comes from the Normal Table).

Confidence interval for NNT

For a sample of 100 people drawn at random from a population (which may number in the millions), then repeat the NNT calculation for a different sample of 100 people, do we expect the first and second NNT estimates to be EXACTLY the same number? No, but we do expect them to be close and we can define what we mean by close as we expect each estimate to be within certain limits. While we expect the second calculation to be close to the first estimate, we would be surprised if it was EXACTLY the same. And so, which is the correct estimate, the first or the second? They both are, in the sense that they both estimate the parameter NNT (a property of a population). But we can do better than two estimates. Confidence Intervals (CI) allow us to assign a probability to how certain we are about the statistic and whether it is likely to be close to the true value. We will

For CI of NNT, we need sample size for control and treatment groups; like all confidence intervals, we need to calculate the standard error of the statistic, in this, case, the standard error (SE) for NNT.

SE = sqrt(risk placebo * (1 - risk placebo) / (# in placebo group) + risk treatment * (1 - risk treatment) / (# in treatment group))

where SE is the standard error for NNT

The CI is approximately then NNT \pm 2 X SE

* – the “2” is only approximate; you need to use Z = 1.965, the value at probability value = 0.9725 (by multiplying this, which comes from the Standard Normal Table).

Odds ratio Standard error and 95% confidence interval

Like any statistic we can calculate, an estimate of odds ratio should be accompanied by the confidence limit. The standard error may be calculated with the following formula

    \begin{align*} SE\left \{ ln\left ( OR \right ) \right \}=\sqrt{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}} \end{align*}

R code

seOdds <- sqrt(sum(1/612, 1/2192,1/375,1/2543))

where ln refers to the natural logarithm. An estimate for the 95% confidence interval is

    \begin{align*} lower \ limit = exp\left (ln\left ( OR \right ) \right )-1.96\cdot SE\left \{ ln\left ( OR \right ) \right \} \end{align*}

where exp is the exponential function 

    \[e^{x}\]

and ln is natural logarithm.

R code

 exp(log(1.89,base=exp(1)) - 1.96*seOdds)

Our example the lower limit was 1.64. For the upper limit

    \begin{align*} upper \ limit = exp\left (ln\left ( OR \right ) \right )+1.96\cdot SE\left \{ ln\left ( OR \right ) \right \} \end{align*}

Our example the upper limit was 2.19.

R code

 exp(log(1.89,base=exp(1)) + 1.96*seOdds)

Thus, our estimate was 1.89 and the 95% confidence interval was \left ( 1.64,2.19\right )

which does not include one. Therefore, we conclude statistically different.

Questions

1. Instead of 95% confidence interval, obtain the 99% confidence interval for odds ratio 1.89

2. What would be the value of Z used for a 99% confidence interval for ARR and NNT?

Chapter 7 contents