6.5 – Discrete probability distributions

Binomial distribution

Discrete refers to particular outcomes. Discrete data types include all of the categorical types we have discussed, including binary, ordinal, and nominal.
The binomial probability distribution is a discrete distribution for the number of successes, k, in a sequence of n independent trials, where the outcome of each trial can take on only one of two possible outcomes. For cases of 0 or 1, yes or no, “heads” or “tails,” male or female, we talk about the binomial distribution, because the outcomes are discrete and there can be only two possible (binary) outcomes.

Fair coins have two sides; tossing a coin we expect “heads” or “tails,” but rarely, some coin types (e.g., USA nickels) may land and come to rest on edge or side. We still consider the coin toss having binary outcomes, by definition, even though a coin may land on edge about one toss in six thousand (Murray and Teare 1993) because the exception is extremely rare. h/t Dr. Jerry Coyne.

The mathematical function of the binomial is written as

    \begin{align*} Pr\left [ X \ successes \right ] = \left ( \frac{n}{X} \right )p^X \left ( 1-p \right )^{n-X} \end{align*}

where the binomial coefficient is given by

    \begin{align*} \left ( \frac{n}{X} \right ) = \frac{n!}{X!\left (n-X \right )!} \end{align*}

and X refers to the number of ways to choose “success” from n observations.

Consider an example.

We have to define what we mean by success. For coin toss, this might be the number of heads.

The mean for the binomial this is given simply as

    \begin{align*} \mu_{X} = np \end{align*}

where X is “Heads” (the category of successes for our example), and p corresponds to the probability the selected event occurs, in this case, “Heads.”

The variance of the binomial distribution is given by

    \begin{align*} \sigma_{X}^{2} = np\left ( 1-p \right ) \end{align*}

Here’s a density plot of two trials with success 2% with n (x) equal to 20 (Fig. 1).

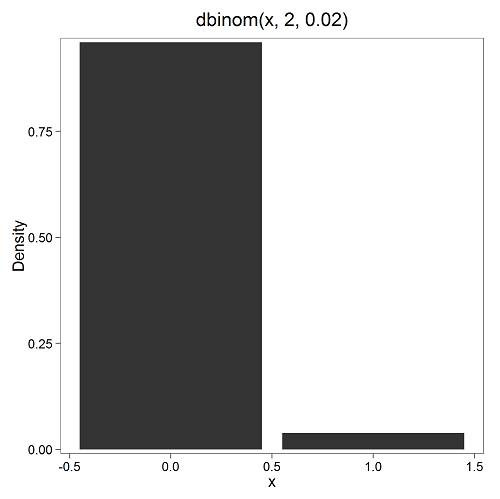
plot generated with KMggplot2 Rcmdr plugin

Figure 1. plot generated with KMggplot2 Rcmdr plugin

Here’s the R code

Create the trials, 1 through 20, then create an object to hold the number of trials

nSize=1:20
Size <- length(nSize); Size

R returns

[1] 20

Assign the probability value to an object

prob <- 0.02

Next, calculate the mean, mu, and the variance, var, for the binomial with prob = 0.02 and number of trials Size = 20

mu <- Size*prob
var <- Size*prob*(1-prob)

Print the mean and variance; lets assign them to an object then print the object

stats <- c(mu, var); stats

And R returns

[1] 0.400 0.392

And here’s a real-world example. Twinning in humans is rare. In Hawaii in the 1990’s the rate of twin births (monozygotic and dizygotic) was about 20 for every 1000 births or 2%. “Success” here then is twin births.

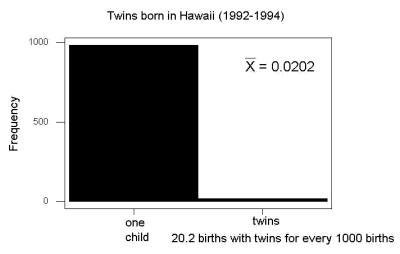
Figure 2. Example of binomial-like distribution: reported twins born in Hawaii.

Figure 2. Example of binomial-like distribution: reported twins born in Hawaii.

Interestingly, rates of twins have since increased in Hawaii (31 out of 1000 births) and in the United States overall (33 out of 1000 births) (Table 2, NCHS Data Brief No. 80, 2012). Data were for year 2009.

Out of 10 births, what is the probability of two twin births in Hawaii?

    \begin{align*} Pr\left [ 2 \ twinbirths \right ] = \left ( \frac{10}{2} \right ) 0.031^2 \left ( 1 - 0.031 \right )^{10-2} \end{align*}

You can solve this with your calculator (yikes!), or take advantage of online calculators (GraphPad QuickCalcs), or use R and Rcmdr.

In R, simply type at the prompt

dbinom(2,10,0.031)
[1] 0.03361446

Try in R Commander.

Rcmdr → Distributions → Discrete distributions → Binomial distribution → Binomial probabilities …

Rcmdr, enter Binomial probabilities

Figure 3. Rcmdr menu to get binomial probability

Note I used p = 0.033 the rate for entire USA. Here’s the output

> .Table <- data.frame(Pr=dbinom(0:10, size=10, prob=0.033))
> rownames(.Table) <- 0:10
> .Table
Pr
0  7.149320e-01
1  2.439789e-01
2  3.746728e-02 ← Answer, 0.0375 or 3.75%
3  3.409639e-03
4  2.036263e-04
5  8.338782e-06
6  2.371422e-07
7  4.624430e-09
8  5.918028e-11
9  4.487991e-13
10 1.531579e-15

And here is the output for our example from Hawaii (p = 0.031).

> .Table <- data.frame(Pr=dbinom(0:10, size=10, prob=0.031))
> rownames(.Table) <- 0:10
> .Table
Pr
0  7.298570e-01
1  2.334940e-01
2  3.361446e-02 ← Answer, 0.0336 or 3.36%
3  2.867694e-03
4  1.605494e-04
5  6.163507e-06
6  1.643178e-07
7  3.003893e-09
8  3.603741e-11
9  2.561999e-13
10 8.196283e-16

We use the binomial distribution as the foundation for the binomial test, i.e., the test of an observed proportion against an expected population level proportion in a Bernoulli trial.

Hypergeometric distribution

The binomial distribution is used for cases of sampling with replacement from a population. When sampling without replacement is done, the hypergeometric distribution is used. It is the number of successes, k, in a sequence of n independent trials drawn from a fixed population. This sampling scheme means that each draw is no longer independent — with each draw you decrease the remaining number of observations and thus change the proportion.

The mathematical function of the hypergeometric is written as

    \begin{align*} Pr\left [X = k \right ] = \frac{\left ( \frac{K}{k} \right )\left ( \frac{N - K}{n - k} \right )}{\left ( \frac{N}{n} \right )} \end{align*}

where N is the population size, K is the number of successes in that population, and n and k are defined as above. Lets look apply this to the twinning problem.

In 2009, 2200 women gave birth in Hawaii County, Hawaii. Out of 10 births, what is the probability of 2 twin births in Hawaii?

Assuming “risk” of twinning is the same rate as in rest of USA, then we have expected 72 successes in this population (0.033 * 2200).

Here’s the graph (Fig. 4).

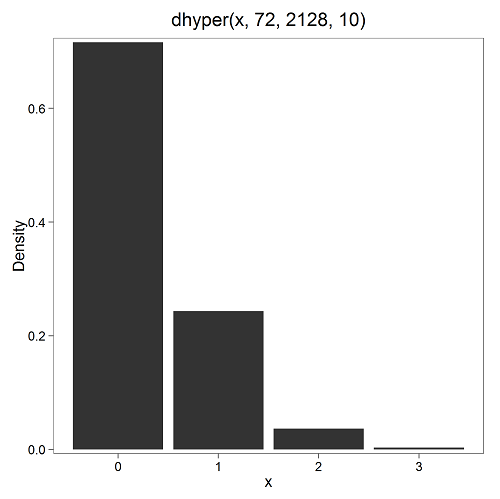
hypergeometric distribution twinning Hawaii

Figure 4. Plot of hypergeometric distribution twinning Hawaii.

where the X axis values shows the number of events with successes (twin births). Taking the bin 2 (we wanted to know about probability of 2 out of ten), we can draw a line back to the Y-axis to get our probability — looks like about 5% roughly. Plot drawn with KMggplot2

To get the actual probability,

Rcmdr → Distributions → Discrete distributions → Hypergeometric distribution → Hypergeometric probabilities …

Rcmdr menu get hypergeometric probability

Figure 5. Rcmdr menu to get hypergeometric probability

where m is the number of successes, n is the number of “failures,” and k is the number of trials.

> .Table
Pr
0 0.716453457
1 0.243438645
2 0.036688041 ← Answer, 0.0367 or 3.67%
3 0.003228871

The reference to white and black balls and urns is a device described by Bernoulli himself and has been used by others ever since to discuss probability problems (called the urn problem) and so I apply it here to be consistent. The urn contains a number of white (x) and a number of black (y) balls mixed together. One ball is drawn randomly from the urn — what color is it? The ball is then is either returned into the urn (replacement) or it is left out (without replacement) as in the hypergeometric problem, and the selection process is repeated.

Besides applications in gambling and balls-in-urns problems, this distribution is the basis for many tests of gene enrichment from microarray analyses. The hypergeometric forms the basis of the Fisher Exact test (see Chapter 9.5).

Discrete uniform distribution

For discrete cases of “1,” “2,” “3,” “4,” “5,” or “6,” on the single toss of fair dice, we can talk about the discrete uniform distribution because all possible outcomes are equally likely. If you are branded as a “card-counter” in Las Vegas, all you’ve done is reached an understanding of the uniform distribution of card suits!

One biological example would be the fate of a random primary oocyte in the human (mammal) female — three out of four will become polar bodies, eventually reabsorbed, whereas one in four will develop into a secondary oocyte (egg); the uniform distribution has to do with the counts of the products — each of the four primary oocytes has the same (apparently) chance (25%) of becoming the egg.

The uniform distribution exists also for continuous data types.

Poisson distribution

An extension from the binomial case is that, rather than following success or failure, you may have the following scenario. Consider a wind-dispersed seed released from a plant. If we markup the area around the plant in grids, we could then count the number of seeds within each grid. Most grids will have no seeds, some grids will have one seed, a few grids may have two seeds, etc. Multiple seeds in grids is a rare event. The graph might look like

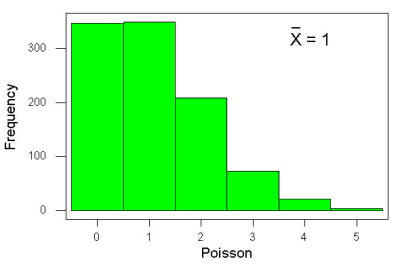
the number of wind-dispersed seeds within each grid

Figure 6. Example, poisson-like graph: the number of wind-dispersed seeds within each grid.

The Poisson has interesting properties, one being that the expected mean is equal to the variance. An equation is

    \begin{align*} Pr\left [X\right ] = \frac{\mu^X e^{-\mu}}{X!} \end{align*}

where μ is the mean (or could substitute with variance!), e is the natural logarithm, and X is number of successes you are interested in. For example, if μ = 1, what is the probability of observing a grid with five seeds? Simple enough to do this by hand, but let’s use Rcmdr instead. Here’s the graph (Fig. 7) from Rcmdr (KMggplot2 plugin)

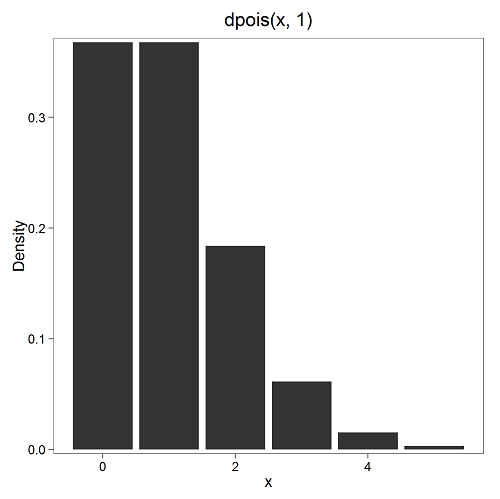
poisson plot, mean = 1

Figure 7. ggplot2 poisson μ= 1.

and for the actual probability we have from R

dpois(5, lambda = 1)
[1] 0.003065662

Rcmdr → Distributions → Discrete distributions → Poisson distribution → Poisson probabilities … (Fig. 8)

The only thing to enter is the mean (some call μ lambda with symbol λ).

Rcmdr menu calculate poisson probability

Figure 8. Rcmdr menu, poisson probability

Here’s the output from R. For intervals 0, 1, 2, 3, …, 6 (Rcmdr just enters this range for you!

> .Table <- data.fram(Pr=dpois(0:6, lambda = 1))
> rownames(.Table) <- 0:6
> .Table
Pr
0 0.3678794412
1 0.3678794412
2 0.1839397206
3 0.0613132402
4 0.0153283100
5 0.0030656620 ← Answer, 0.0307 or 3.07%
6 0.0005109437

Next — Continuous distributions

And finally, for ratio (continuous) scale data, which can take on any value, we can express the chance that probability of a given point as a continuous function, with the normal distribution being one of the most important examples (there are others, like the F-distribution). Many statistical procedures assume that the data we use can be viewed as having come from a “normally distributed population.” See Chapter 6.6.

Questions

1. For each of the following scenarios, identify the most likely distribution that may be assumed

  • litter size of 100 toy poodle females. A toy poodle is a purebred dog breed: range of litter size is 1 – 4 pups (Borge et al 2011)
  • Mean litter size and total number of litters born per season of the year for litters registered within The Norwegian Kennel Club in 2006 and 2007: means by season were Fall 5, Winter 5, Spring 5, Summer 5 (Borge et al 2011)
  • C-reactive protein (CRP) blood levels may increase when a person has any number of diseases that cause inflammation. Although CRP is reported as mg/dL, Doctors evaluate a patient’s CRP status as all measures below 1.0 are normal, all measures above 1 are above 1.0.

2. Quarterback sacks by game for the NFL team Seahawks, years 2011 through 2022 are summarized below (data extracted from https://www.pro-football-reference.com/ ).

Sacks How many
games?
0 25
1 46
2 49
3 39
4 25
5 14
6 8
7 2
8 1
9 0

a) Assuming a Poisson distribution, what are the mean (lambda) and variance?

b) The table covers a total of 112 games. How many sacks (events) were observed?

c) What is the probability of the Seahawks getting zero sacks in a game (in 2022, a season was 17 games; prior years a season was 16 games)?

Chapter 6 contents