17.2 – Relationship between the slope and the correlation

Introduction

Product moment correlation is used to indicate the direction and the strength of the linear association between two ratio-scale variables; the slope tells you the rate of change between the two variables. When the correlation is negative, the slope will be negative; when correlation is positive, so too will the slope.

As you might suspect, there is a mathematical relationship between the product moment correlation, r, and the regression slope, b1. We haven’t spent much time explaining the equations presented in this text, but correlation and linear regression are such important tools it’s worth a closer look.

Recall from our discussion in Chapter 16.1, the equation of the correlation is

    \begin{align*} r_{XY}=\frac{\left (X-\bar{X} \right )\left (Y-\bar{Y} \right )}{\left (n-1 \right )s_{X} s_{Y}} \end{align*}

where the numerator is termed the covariance between X and Y and the denominator contains the standard deviations of X and Y variables. We can say the at the covariance is standardized by the variability in X and Y. In contrast, the regression slope is equal to the covariance divided by the variance in X.

    \begin{align*} b_{1}=\frac{\sum_{i=1}^{n}\left (X-\bar{X} \right )\left (Y-\bar{Y} \right )}{\sum_{i=1}^{n}\left (n-1 \right )s_{X} s_{Y}} \end{align*}

Thus, with a little algebra, we can see that the slope and correlation are equal to each other as

    \begin{align*} b_{1}=r\cdot \frac{s_{X}}{s_{Y}} \end{align*}

This should drive home the following statistical reasoning point. You can always calculate a slope from a correlation, but recall that correlation analysis is intended as a test of the hypothesis of a linear association between variables for which cause and effect model — though perhaps reasonable — should be implied. Just because it is mathematically possible does not mean the analysis is correct for the problem.

Coefficient of determination and the Product moment correlation

R^2, the coefficient of determination, was introduced in the last chapter. It’s the ratio of variation of the data explained by the linear regression model divided by the total variation in the data. Values range from 0% to 100% — it’s a measure of fit, how well the data are described by a line. Note that part of our description for r, the product moment correlation — strength of the linear association — is simply another way to describe model fit. Thus,

    \begin{align*} r =\sqrt{R^2} \end{align*}

Of course, we lose the direction information by squaring the correlation.

Questions

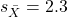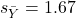  1. If the correlation is 0.6, s_{\bar{X}}=2.3, and s_{\bar{Y}}=1.67, what is the slope estimate?

Chapter 17 contents