6.11 – F distribution

Introduction

The F distribution is the probability distribution associated with the F statistic and named in honor of R. A. Fisher. The F distribution is used as the null distribution of the ANOVA test statistic. The F distribution is the ratio of two chi-square distributions, with degrees of freedom v1 and v2 for numerator and denominator, respectively.

We can for illustration purposes define the F statistic as a ratio of two variances,

    \begin{align*} F = \frac{s_{2}^2}{s_{1}^2} \end{align*}

The F statistic has two sets of degrees of freedom, one for the numerator and one for the denominator. The actual formula for the F distribution is quite complicated and in general we don’t use the F distribution in a way that involves parameter estimation. Rather, it is used in evaluating the statistical significance of the F statistic. Therefore, we produce but a few graphs and a table of critical values to illustrate the distribution.

We call the result of this calculation the F test statistic. We evaluate how often that value or greater of a test statistic will occur by applying the F distribution function. A few graphs to get a sense of what the distribution looks like for varying v1, v2 held to ten degrees of freedom (Fig. 1).
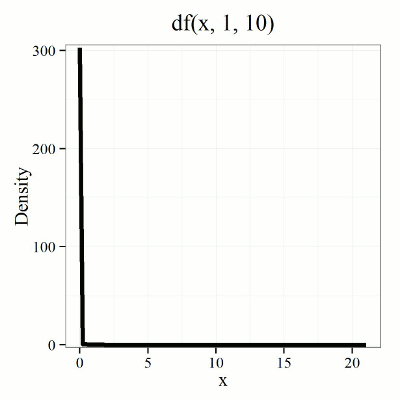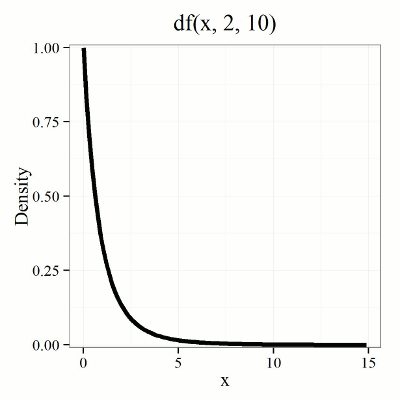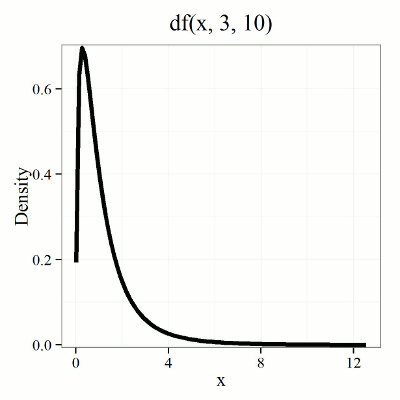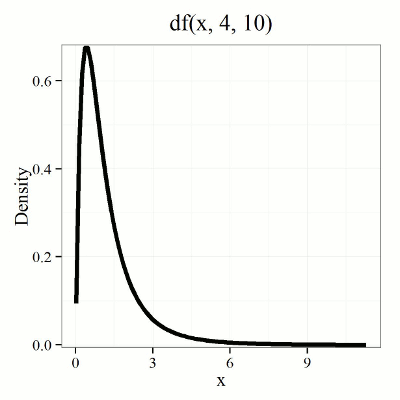
animated GIF, F distribution

 

Figure 1. Animated GIF plot of F distribution value for range of degrees of freedom.

By convention in the Null Hypothesis Significance Testing protocol (NHST), we compare the test statistic to a critical value. The critical value is defined as the value of the test statistic that occurs at the Type I error rate, which is typically set to 5%., per our presentations in Chapter 6.7, 6.9, and 6.10. The justification for NHST approach to testing of statistical significance is developed in Chapter 8.

Table of Critical values of the F distribution, one tail (upper)

Degrees of freedom v1 = 1 – 4, v2 = 10

Fv1, 10 α = 0.05 α = 0.025 α = 0.01
1 4.964 6.937 10.044
2 4.103 5.456 7.559
3 3.708 4.826 6.552
4 3.478 4.468 5.994

For the complete F table see Appendix 20.4

χ2, t and F distributions are related

χ2, t and F distributions are all distributions indexed by their degrees of freedom. With some algebra, these three distributions can be shown to be related to each other. The probabilities tabled in the chi-squared are part of the F-distribution.

Some interesting relationships between the F distribution and other distributions can be shown. By definition we claimed that the F distribution is built on ratio of chi-square distributions, so that should indicate to you the relationship between the two kinds of continuous probability distributions. However, one can also show relationships to other distributions for the F distribution. For example, for the case of v1 = 1 and v2 = any value, then F1,v2 = t2, where t refers to the t distribution.

Questions

  1. What happens to the shape of the F distribution as degrees of freedom are increased from 1 to 5 to 20 to 100?
  2. In Rcmdr, which option do you select to get the critical value for df1 = 1 and df=20 at alpha = 5%?
    A. F quantiles
    B. F probabilities
    C. Plot of F distribution
    D. Sample from F distribution

Be able to answer these questions using the F table, Appendix 20.4, or using Rcmdr

  1. For probability α = 5%, and numerator degrees of freedom equal to 1, what is the critical value of the F distribution (upper tail) for 1 degree of freedom? For 5 df? For 20 df? For 30 df?
  2. The value of the F test statistic is given as 12. With 3 degrees of freedom for the numerator, and ten degrees of freedom for the denominator, what is the approximate probability of this value, or greater from the F distribution?

Chapter 6 contents