11.5 – Power analysis in R
Introduction
In R, you can estimate the
- Statistical power — how probable are you to correctly reject the null hypothesis
- Sample size — how many samples or observations must we get to have a reasonable chance to correctly reject a null hypothesis
- Effect size (minimum difference) — how different are the two samples?
Power analysis is recommended before conducting an experiment, but it is also valuable after an experiment.
Base R and pwr package
In Chapter 11.4 we presented functions from BSDA package. R (but not Rcmdr — see the EZR plugin described below) provides all of the basic power analysis we would need for t-tests, one-way ANOVA, etc. as part of the base installation (Everitt and Hothorn 2007). However, the package pwr, provides a more comprehensive package for power analysis. Load and install the R package pwr.
For example, to determine the number of samples for an independent sample t-test (two-tailed), the function is pwr.t.test().
pwr.t.test(n = NULL, d = NULL, sig.level = 0.05, power = NULL, type = c("two.sample", "one.sample", "paired"), alternative = c("two.sided", "less","greater"))
Table 1. Components of pwr.t.test().
| n | Number of observations (per sample) |
| d | Effect size |
| sig.level | Significance level (Type I error probability) |
| power | Power of test (1 minus Type II error probability) |
| type | Type of t test : one- two- or paired-samples |
| alternative | a character string specifying the alternative hypothesis, must be one of “two.sided” (default), “greater” or “less |
The basic question is, how many samples (observations) do I need for each group (k) at Type I error of 5% and type II error of 95%?
To run the test, you fill in all of the “NULL” except the one you wanted solved (i.e., leave n = NULL).
For an effect size of 0.2, Type I error (significance level) of 5%, and 95% power, how many observations per group do we need for our study?
pwr.t.test(n = NULL, d =0.2, sig.level = 0.05, power = 0.95, type = c("two.sample"), alternative = c("two.sided"))
Two-sample t test power calculation
n = 650.6974
d = 0.2
sig.level = 0.05 power = 0.95 alternative = two.sided
note: n is number “n” in each group
Wow!
The R pwr package is not as convenient as it could be (have to load and run R scripts): for intro level, try one of the many online sites. Here is a website which can help with power analysis based on a variety of situations. The programs are java-coded. http://www.stat.uiowa.edu/~rlenth/Power/index.html
Note 1: You see what I just did? I “complained” about a free program’s performance! Don’t do that — what I mean by this is that there’s a learning curve with the pwr package, and there are other options to explore outside of the R programming world.
Power analysis with the EZR Rcmdr plugin
The EZR plugin for R Commander provides some facilities to do power analysis (Kanda 2013). First, download and install the RcmdrPlugin.EZR package. The EZR plugin for Rcmdr, RcmdrPlugin.EZR, provides an interface to explore power analyses, along with many other statistical functions (Kanda 2013). After loading the plugin to Rcmdr, additional drop down options are added to the menu bar (Fig 1).
Figure 1. Screenshot of Rcmdr menu bar with (A) and without (B) the EZR plugin.
I’ll demonstrate use of the plugin, but I recommend that you use pwr.t.test() instead. Although EZR uses a drop-down menu system it has many more functions than we need to solve this simple exercise. Thus, EZR is not any easier to apply for what we need here. That said, off we go.
Worked example
Consider a simple data set, wheel running performance in 24-hours for three strains of mice.
Table 2. Wheel running performance in 24-hours for three strains of mice.
| Mouse strain | Average | Standard deviation | n |
| AKR | 395 | 169.7 | 20 |
| CBA | 855 | 77.8 | 20 |
| C57BL/10 | 1135 | 63.6 | 20 |
Consider two groups of mice, AKR vs CBA for wheel running performance. How many samples needed to show a statistical difference for ?
Calculate the pooled standard deviation and calculate a difference between the means (the effect size) for which you wish to say is statistically different. For this example, 132.0 and 460, respectively. With EZR plugin installed and active in R Commander (Fig 2), select
Rcmdr: Statistical analysis → Calculate sample size → Calculate sample size for comparison between two means
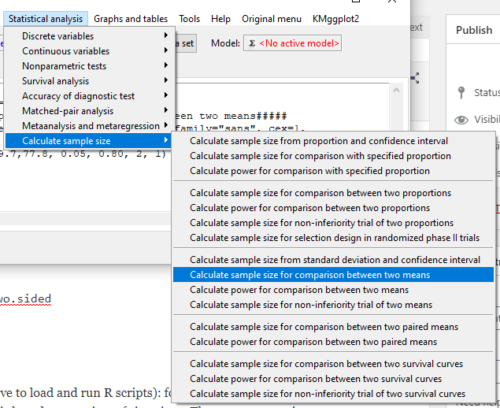
Figure 2. Screenshot of Rcmdr EZR plugin menu.
Select Calculate sample size for comparison between two means, enter the effect size (difference in sample means), standard deviation in each group (or a single value for pooled standard deviation) (Fig 3).
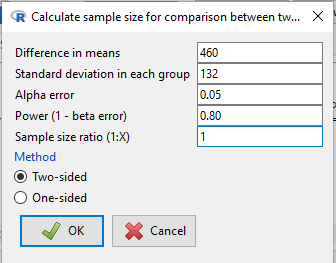
Figure 3. Screenshot of EZR Menu to obtain sample size for the comparison between two (sample) means.
R output from EZR Calculate sample size for comparison between two means
Assumptions Difference in means 460 Standard deviation 132 Alpha 0.05 two-sided Power 0.8 N2/N1 1 Required sample size Estimated N1 2 N2 2
Questions
Recall lizard body mass data set from Chapter 10.1
Geckos <- c(3.186, 2.427, 4.031, 1.995) Anoles <- c(5.515, 5.659, 6.739, 3.184)
Enter the data into an R data.frame, carry out the independent sample t-test, then
- Calculate power for the comparison between the two means
- Calculate sample size needed to achieve 95% power.
Quiz Chapter 11.5
Power analysis in R