12.5 – Effect size for ANOVA
Introduction
As noted in the t-test chapter and our discussion of statistical power, an effect size is a measure of the strength of a phenomenon. An effect size calculated from data is a descriptive statistic that indicates how large (or small) the difference is between two or more samples. Effect size measures help to provide context between statistical significance, i.e., p-values. Among other uses, effect size measures play an important role in meta-analysis studies biological significance (i.e., importance of the measured difference).
Estimation of effect size
eta-squared (η2)
![]()
where SSB and SST are from the one-way ANOVA and refer to the sum of squared among (between) groups and the total sum of squares, respectively. ![]() measures the proportion of the variation in the response variable that can be explained by membership in one of the groups.
measures the proportion of the variation in the response variable that can be explained by membership in one of the groups.
For example, ![]() of 0.15 or 15% is interpreted to mean that just 15% of the variation in the response variable can be attributed to membership in the groups (i.e., whether a subject was in control group or treatment group, only 15% of the differences between individuals can be attributed to having received control).
of 0.15 or 15% is interpreted to mean that just 15% of the variation in the response variable can be attributed to membership in the groups (i.e., whether a subject was in control group or treatment group, only 15% of the differences between individuals can be attributed to having received control).
Note 1: η2 is just the unadjusted coefficient of determination, R2.
omega-squared (ω2)
A similar, but “less biased” effect size estimate is given by omega-squared (ω2) (Okada 2013). (The bias comes in because sample estimates were used.) Interpretation of ![]() is the same as
is the same as ![]() : measures the proportion of variation explained by membership in the groups.
: measures the proportion of variation explained by membership in the groups. ![]() is given as
is given as
![]()
The bias for ![]() is more pronounced with small sample size, so omega-squared is preferred.
is more pronounced with small sample size, so omega-squared is preferred. ![]() will always be less than or equal to
will always be less than or equal to ![]() (Okada 2013).
(Okada 2013).
R code
If you have not already done so, please install the package effectsize.
We’ll use the example one-way ANOVA problem from Chapter 12.2. I’ve added the data as example.ch12 and some R script to load the data, scroll to bottom of this page or click on the link).
Get 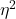
First, get the ANOVA model. There are several ways to do this within R (and Rcmdr), the most general is to use the general linear model function, lm(),
#Get the model AnovaModel.4 <- lm(Difference~Group, data=example.ch12) #turn it into format that the next command needs aov_fit <- anova(AnovaModel.4) #get eta effectsize(aov_fit)
R output
Parameter | Eta2 (partial) | 9e+01% CI ----------------------------------------- Group | 0.95 | [0.88, 0.97]
![]() is 0.95 for the Difference group.
is 0.95 for the Difference group.
Get 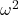
R code
omega_squared(aov_fit, partial = FALSE, ci = 0.95)
R output
Parameter | Omega2 | 1e+02% CI --------------------------------- Group | 0.93 | [0.82, 0.97]
This is a case of a large effect due to group membership. The differences between A, B, and C means account for 93% of the variation. Note that both ![]() and
and ![]() are close; note also that
are close; note also that ![]() is greater than
is greater than ![]() .
.
Questions
- In Chapter 7.4 we introduced the concept of number needed to treat, NNT. Discuss the concept of “important differences” between sample means of a control group and a treatment group to NNT.
- This question refers to hypothetical data presented in Chapter 12.2. For the “No difference” group, calculate
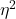 and
and 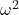 . Use the boxplots shown in Figure 1, together with effect size statistics to discuss the relationship between statistical significance (p-value) and important difference.
. Use the boxplots shown in Figure 1, together with effect size statistics to discuss the relationship between statistical significance (p-value) and important difference.
Quiz Chapter 12.5
Effect size for ANOVA
Data set
example.ch12 <- read.table(header=TRUE, sep=",",text=" Group, No.difference, Difference A, 12.04822, 11.336161 A, 12.67584, 13.476142 A, 12.99568, 12.961210 A, 12.01745, 11.746712 A, 12.34854, 11.275492 B, 12.17643, 7.167262 B, 12.77201, 5.136788 B, 12.07137, 6.820242 B, 12.94258, 5.318743 B, 12.07670, 7.153992 C, 12.58212, 3.344218 C, 12.69263, 3.792337 C, 12.60226, 2.444438 C, 12.02534, 2.576014 C, 12.60420, 4.575672") #check the dataframe head(example.ch12)