12.4 – ANOVA from “sufficient statistics”

Introduction

By now you should be able to run a one-way ANOVA using R (and R Commander) with ease. As a reminder, You should also be aware that, if you need to, you could use spreadsheet software like Microsoft Excel or LibreOffice Calc to run one way ANOVA on a small data set. Still, there are times when you may need to run a one-way ANOVA on a small data set, and doing so by hand calculator may be just as convenient. What are your available options?

Following the formulas I have given would be one way to calculate ANOVA by hand, but it would be tedious and subject to error. Instead of working with the standard formulas, calculator shortcuts can be derived with a little algebra and this is where I want to draw your attention now. This technique will come in handy in lab classes or other scenarios where you collect some data among a set number of groups and calculate means and standard deviations. The purpose of this posting is to show you how to obtain the necessary statistics to calculate a one-way ANOVA from the available descriptive statistics: means, standard deviations, and sample sizes. In other words, these are the sufficient statistics for one-way ANOVA.

Note in Chapter 11.5, we introduced use of summary statistics, i.e., “sufficient statistics,” to calculate the independent sample t-test.

As you recall, a one-way ANOVA yields a single F test of the null hypothesis that all group means are equal. To calculate the F test, you need

  • Mean Square Between Groups, MS_{B}
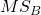
  • Mean Squares Within Groups or Error, MS_{E}

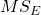
F is then calculated as

    \begin{align*} F = \frac{MS_{B}}{MS_{E}} \end{align*}

with degrees of freedom k – 1 for the numerator and N – 1 for the denominator. MS_{E} can also appear as MS_{W}

We can calculate MS_{B} as

    \begin{align*} MS_{B} = \frac{\sum_{i=1}^{k}n_{i}\left ( \bar{X}_{i}-\bar{X}_{G} \right )^2}{k-1} \end{align*}

where k is the number of i th groups, ni is the sample size of the ith group,  \bar{X}_{G} refers to the overall mean for all of the  \bar{X}_{i} sample means.

Next, for the Error Mean Square, MS_{E}, all we need is the average of the sample variances (the square of the sample standard deviation, s).

    \begin{align*} MS_{E} = \frac{\sum_{i=1}^{k}s_{i}^2}{k} \end{align*}

ANOVA from sufficient statistics

Consider an example data set (Table 1) for which only summary statistics are available (mean and standard deviation, sd). The data set is for metabolic rate (ml oxygen per hour) for strains of laboratory mice. Sample size for each group was seven mice.

Table 1. Descriptive statistics wheel-running behavior mice from ten different inbred strains of mice (Mus domesticus).

Strain n Mean sd
AKR 7 395 169.7
C57BL_10 7 1135 63.6
CBA 7 855 77.8
129S1 7 1012 176.8
C3H/He 7 833 49.5
C57BL/6 7 1075 91.9
FVB/N 7 1023 91.9
A 7 806 134.4
BALB/c 7 936 70.7
DBA/2 7 872 49.5

Spreadsheet calculations

You have several options at this point, ranging from using your calculator and the formulas above (don’t forget to square the standard deviation to get the variances!), or you could use Microsoft Excel or LibreOffice Calc and enter the necessary formulas by hand (Table 2). You’ll also find many online calculators for one-way ANOVA by sufficient statistics (e.g., https://www.danielsoper.com/statcalc/calculator.aspx?id=43).

Table 2. Spreadsheet with formulas for calculating one-way ANOVA from means and standard deviations from statistics presented in Table 1.

  A B C D E F G H I
1 Strain n Mean sd squared variance   grand
mean		 =AVERAGE(C:C)
2 AKR 7 395 169.7 =B2*(C2-$I$1)^2 =D2^2 dfB =COUNT(B:B)-1
3 C57BL_10 7 1135 63.6 =B2*(C3-$I$1)^2 =D3^2 dfE =SUM(B:B)-I2
4 CBA 7 855 77.8 =B2*(C4-$I$1)^2 =D4^2 Msb =SUM(E:E)/(COUNT(E:E)-1)
5 129S1 7 1012 176.8 =B2*(C5-$I$1)^2 =D5^2 Mse =SUM(F:F)/COUNT(F:F)
6 C3H/He 7 833 49.5 =B2*(C6-$I$1)^2 =D6^2 F =I4/I5
7 C57BL/6 7 1075 91.9 =B2*(C7-$I$1)^2 =D7^2 P-value =FDIST(I6,I2,I3)
8 FVB/N 7 1023 91.9 =B2*(C8-$I$1)^2 =D8^2
9 A 7 806 134.4 =B2*(C9-$I$1)^2 =D9^2
10 BALB/c 7 936 70.7 =B2*(C10-$I$1)^2 =D10^2
11 DBA/2 7 872 49.5 =B2*(C11-$I$1)^2 =D11^2

For this example, you should get the following

MSB = 299943.5

MSE = 11500.8

F = 26.08

P-value = 9.75E-18

Note: The number of figures reported for the P-value implies a precision that the data simply do not support. For a report, recommend writing the P-value < 0.001

But, R can do it better.

Here’s how. Install the HH package (or RcmdrPlugin.HH for use in Rcmdr) and call the aovSufficient function.

Step 1. Install the HH package from a CRAN mirror, e.g., cloud.r-project.org, in the usual way.

chooseCRANmirror()
install.packages("HH") 
library(HH)

Step 2. Enter the data. Do this in the usual way (e.g., from a text file), or enter directly using the read.table command as follows.

MouseData <- read.table(header=TRUE, sep = "", text= 
"Strain Mean sd
AKR 395 169.7
C57BL_10 1135 63.6
CBA 855 77.8
129S1 1012 176.8
C3H/He 833 49.5
C57BL/6 1075 91.9
FVB/N 1023 91.9
A 806 134.4
BALB/c 936 70.7
DBA/2 872 49.5") 
#Check import
head(MouseData)

End of R input

I know, a little hard to read, but from the MouseData to the end bracket “) before the comment line #Check import, that’s all one command.

Of course, you could copy the data and import the data from your computer’s clipboard in Rcmdr: Data → Import data → from text file, clipboard, or URL…  (Hint: for field separator, try White space; if that fails, try Tabs).

Once the data set is loaded, proceed to Step 3.

Step 3. In our example, sample size is included for each group. Skip to step 4. If, however, the table lacked the sample size information, you can always add a new variable. For example, if we needed to add sample size to the data frame, we would use the repeat element function, rep().

MouseData$n <- rep(7, 10)

If you check the View data set button in Rcmdr, you will see that the command in Step 3 has added a new variable “n” for each of the eleven rows. The function rep() stands for “replicate elements in vectors” and what it did here was enter a value of 7 for each of the ten rows in the data set. Again, this step is not necessary for this example because sample size is already part of the data frame. Proceed to step 4.

Step 4. Run the one way ANOVA using the sufficient statistics and the HH function aovSufficient

MouseData.aov <- aovSufficient(Mean ~ Strain, data=MouseData)

Step 5. Get the ANOVA table

summary(MouseData.aov)

Here’s the R output

            Df  Sum Sq  Mean Sq  F value  Pr(>F) 
Strain       9 2699491   299943    26.08  <2e-16 ***
Residuals   60  690046    11501 
----
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

End R output

To explore other features of the package, type ?aovSufficient at the R prompt (like all R functions, extensive help is generally available for each function in a package).

Limitations of ANOVA from sufficient statistics

This was pretty easy, so it is worth asking — Why go through the bother of analyzing the raw data, why not just go to the summary statistics and run the calculator formula? First, the chief reason against the calculator formula and use of only sufficient statistics loses information about the individual values and therefore you have no access to the residuals. The residual of an observation is the difference between the original observation and the model prediction. The residuals are important for determining whether the model fits the data well and are, therefore, part of the toolkit that statisticians need to do proper data analysis. We will spend considerable time looking at residual patterns and it is an important aspect of doing statistics correctly.

Secondly, while it is possible to extend this approach to more complicated ANOVA problems like the two-way ANOVA (Cohen 2002), the statistical significance of the interaction term(s) calculated in this way are only approximate (the main effects are OK to interpret). Thus, ANOVA from sufficient statistics has its place when all you have is access to descriptive statistics, but its use is limited and not at all the preferred option for data analysis when the original, raw observations are in hand.

Questions

1. Under what circumstances would you use “sufficient statistics” to calculate a one-way ANOVA?

2. Calculate the one-way ANOVA for body weight of 47 female (F) and 97 male (M) cats (kilograms, dataset cats in MASS R package) from the following summary statistics.

n Mean sd
F 47 2.36 0.274
M 97 2.9 0.468

3. Bonus: Load the cats data set (package MASS, loaded with Rcmdr) and run a one-way ANOVA using the aov() function via Rcmdr. Are the ANOVA from sufficient statistics the same as results from the direct ANOVA calculation? If not, why not.

Chapter 12 contents