18.4 – Generalized Linear Squares
Introduction
With access to powerful computers and better algorithms, we can move past the classical ANOVA and ordinary least squares approaches to linear models. We have discussed general linear models, but here we introduce generalized linear models, GLM. The chief advantage of these approaches is that we no longer need to make assumptions about the error variance, for example — now, we can specify the model structure and account for correlated errors and other deviations. What follows on this page is just a brief foray into GLM; for more — and better! discussion, see Zuur et al (2009) and Dobson and Barnett (2018).
Model variances
Data from Corn and Hiesey (1973) ohia.RData
head(ohia) Site Height Width 1 M-1 12.5567 19.1264 2 M-1 13.2019 13.1547 3 M-1 8.0699 16.0320 4 M-1 6.0952 22.8586 5 M-1 11.3879 11.0105 6 M-1 12.2242 21.8102
A reminder, what we did before. Note that # ignore the variance issue
AnovaModel.1 <- aov(Height ~ Site, data = ohia); summary(AnovaModel.1)
Df Sum Sq Mean Sq F value Pr(>F)
Site 2 4070 2034.8 22.63 0.000000131 ***
Residuals 47 4227 89.9
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Alternatively, use gls(). Default fits by restricted maximum likelihood, REML. That is, it’s the likelihood of linear combinations of the original data. This first pass, we ignore issues about error variances, in other words, an approach similar to the ANOVA we did before.
model.aov.1 <- gls(Height ~ Site, data = ohia)
Generalized least squares fit by REML
Model: Height ~ Site
Data: ohia
AIC BIC logLik
361.1312 368.5318 -176.5656
Coefficients:
Value Std.Error t-value p-value
(Intercept) 15.313745 2.120550 7.221591 0.0000
Site[T.M-2] 19.261000 2.998911 6.422666 0.0000
Site[T.M-3] 2.924215 3.672900 0.796160 0.4299
Correlation:
(Intr) S[T.M-2
Site[T.M-2] -0.707
Site[T.M-3] -0.577 0.408
Standardized residuals:
Min Q1 Med Q3 Max
-1.9832938 -0.5020880 -0.1850871 0.5017636 3.0850635
Residual standard error: 9.483388
Degrees of freedom: 50 total; 47 residual
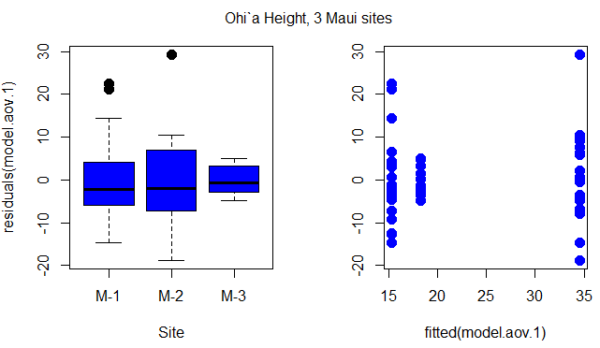
Figure 1. Box plot of residuals from GLS model by elevation site predictors (left) and scatterplot of residuals by fitted values from GLS model (right).
Inspection of Figure 1 suggests residuals not equal — note restricted range of intervals for the M-2 site.
R code for the plot in Figure 1
par(mfrow = c(1, 2))
plot(residuals(model.aov.1) ~ Site, pch=19, cex=1.5,col="blue", data = ohia)
plot(residuals(model.aov.1) ~ fitted(model.aov.1), pch=19, cex=1.5, col="blue", ylab="", data=ohia)
mtext("ANOVA Ohi`a Height, 3 Maui sites ", side = 3, line = -3, outer = TRUE)
So, our conventional approach would be to investigate the assumption of equal error variances.
# test equal variances, Height
leveneTest(Height ~ Site, data=ohia, center="median")
Levene's Test for Homogeneity of Variance (center = "median")
Df F value Pr(>F)
group 2 2.1663 0.1259
47
We would conclude no significant departures from equal variances by Levene test. Consider Bartlett’s test.
bartlett.test(Height ~ Site, data=ohia) Bartlett test of homogeneity of variances data: Height by Site Bartlett's K-squared = 10.373, df = 2, p-value = 0.005592
In conclusion, there’s some evidence of unequal variances. We revisit the Generalized Linear Model approach, this time accounting for unequal variances as part of model
model.aov.3 <- gls(Height ~ Site, data = ohia, weights = varIdent(form = ~1|Site)); summary(model.aov.3)
Generalized least squares fit by REML
Model: Height ~ Site
Data: ohia
AIC BIC logLik
354.421 365.5219 -171.2105
varIdent permits variances for each group to vary.
Results from R continue below.
Variance function:
Structure: Different standard deviations per stratum
Formula: ~1 | Site
Parameter estimates:
M-1 M-2 M-3
1.0000000 1.0396880 0.3471771
We see here that comparisons were carried out versus M-1 site.
Coefficients:
Value Std.Error t-value p-value
(Intercept) 15.313745 2.280931 6.713812 0.0000
Site[T.M-2] 19.261000 3.290358 5.853770 0.0000
Site[T.M-3] 2.924215 2.541027 1.150800 0.2556
Marginal differences between M-1 and M-2 for height were significantly different, but not between M-1 and M-3 site.
Correlation:
(Intr) S[T.M-2
Site[T.M-2] -0.693
Site[T.M-3] -0.898 0.622
Standardized residuals:
Min Q1 Med Q3 Max
-1.7734556 -0.6909962 -0.2108834 0.5801370 2.7586550
Residual standard error: 10.20064
Degrees of freedom: 50 total; 47 residual
# Test the models
> anova(model.aov.1, model.aov.3)
Model df AIC BIC logLik Test L.Ratio p-value
model.aov.1 1 4 361.1312 368.5318 -176.5656
model.aov.3 2 6 354.4210 365.5219 -171.2105 1 vs 2 10.7102 0.0047
Although additional degrees of freedom are required, note that this model (model.aov.3) has higher (better!) log likelihood (-171.21) than model.aov.1, the gls model lacking a fit for different variances (-176.57). Introduce a test of the hypothesis that the two models are equal by comparing the log (natural) likelihoods, the log likelihood ratio test, LRT.
![\begin{align*} LRT=-2\cdot ln\left ( \frac{LL\ model \1}{LL \ model \2} \right ) = -2\cdot ln \left [ \left (LL\ model \1 \right ) - \left (LL \ model \2 \right ) \right ] \end{align*}](https://biostatistics.letgen.org/wp-content/ql-cache/quicklatex.com-a5d504cb562cdafece753076d69c0ed8_l3.png "Rendered by QuickLaTeX.com")
The LRT follows a chi-square distribution (per Wilk’s theorem). If there was no advantage to fitting for unequal variances, then the model fit would not be improved and p-value of the LRT would not be less than 5%.
Conclusion
You can see why this approach, even for the rather simple example in this case, modeling versus separate test of assumptions would be the preferred way to go. We get a better fitting model, and, we have employed proper statistical practice (Dobson and Barnett 2018).
Another example, same data set.
# ignore variances, Width
model.aov.2 <- gls(Width ~ Site, data = ohia); summary(model.aov.2)
Figure 2.
par(mfrow = c(1, 2))
plot(residuals(model.aov.2) ~ Site, pch=19, cex=1.5,col=”blue”, data = ohia)
plot(residuals(model.aov.2) ~ fitted(model.aov.2), pch=19, cex=1.5, col=”blue”, ylab=””, data=ohia)
mtext(“ANOVA Ohi`a Width 3 Maui sites “, side = 3, line = -3, outer = TRUE)
# test equal variances, Width
Tapply(Width ~ Site, var, na.action=na.omit, data=ohia) # variances by group
leveneTest(Width ~ Site, data=ohia, center=”median”)
Tapply(Width ~ Site, var, na.action=na.omit, data=ohia) # variances by group
bartlett.test(Width ~ Site, data=ohia)
# model the variances, Height
library(nlme)
model.aov.3 <- gls(Height ~ Site, data = ohia, weights = varIdent(form = ~1|Site)); summary(model.aov.3)
par(mfrow = c(1, 2))
plot(residuals(model.aov.3) ~ Site, pch=19, cex=1.5,col=”red”, data = ohia)
plot(residuals(model.aov.3) ~ fitted(model.aov.3), pch=19, cex=1.5, col=”red”, ylab=””, data=ohia)
mtext(“GLS Ohi`a Height 3 Maui sites “, side = 3, line = -3, outer = TRUE)
# Test the models
anova(model.aov.1, model.aov.3)
# model the variances, Width
model.aov.4 <- gls(Width ~ Site, data = ohia, weights = varIdent(form = ~1|Site)); summary(model.aov.4)
par(mfrow = c(1, 2))
plot(residuals(model.aov.4) ~ Site, pch=19, cex=1.5,col=”red”, data = ohia)
plot(residuals(model.aov.4) ~ fitted(model.aov.4), pch=19, cex=1.5, col=”red”, ylab=””, data=ohia)
mtext(“GLS Ohi`a Width 3 Maui sites “, side = 3, line = -3, outer = TRUE)
# Test the models
anova(model.aov.2, model.aov.4)
Model correlated residuals
[pending]
Questions
[pending]