17.7 – Regression model fit

Introduction

In Chapter 17.5 and 17.6 we introduced the example of tadpoles body size and oxygen consumption. We ran a simple linear regression, with the following output from R

RegModel.1 <- lm(VO2~Body.mass, data=example.Tadpole)

summary(RegModel.1)

Call:
lm(formula = VO2 ~ Body.mass, data = example.Tadpole)

Residuals:
    Min      1Q    Median       3Q       Max 
-202.26 -126.35     30.20    94.01    222.55

Coefficients:
                Estimate     Std. Error    t value    Pr(>|t|) 
(Intercept)      -583.05         163.97     -3.556     0.00451 ** 
Body.mass         444.95          65.89      6.753   0.0000314 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 145.3 on 11 degrees of freedom
Multiple R-squared: 0.8057, Adjusted R-squared: 0.788 
F-statistic: 45.61 on 1 and 11 DF, p-value: 0.00003144

You should be able to pick out the estimates of slope and intercept from the table (intercept was -583 and slope was 445). Additionally, as part of your interpretation of the model, you should be able to report how much variation in VO2 was explained by tadpole body mass (coefficient of determination, R², was 0.81, which means about 81% of variation in oxygen consumption by tadpoles is explained by knowing the body mass of the tadpole.

What’s left to do? We need to evaluate how well our model fits the data, i.e., we evaluate regression model fit. By fit we mean, how well does our model agree to the raw data? A poor fit and the model predictions are far from the raw data; a good fit, the model accurately predicts the raw data. In other words, if we draw a line through the raw data, a good fit line crosses through most of the points — a poor fit the line rarely passes through the cloud of points.

How to judge fit? This we can do by evaluating the error components relative to the portion of the model that explains the data. Additionally, we can perform a number of diagnostics of the model relative to the assumptions we made to perform linear regression. These diagnostics form the subject of Chapter 17.8. Here, we ask how well does the model,

fit the data?

Model fit statistics

The second part of fitting a model is to report how well the model fits the data. The next sections apply to this aspect of model fitting. The first area to focus on is the magnitude of the residuals: the greater the spread of residuals, the less well a fitted line explains the data.

In addition to the output from lm() function, which focuses on the coefficients, we typically generate the ANOVA table also.

Anova(RegModel.1, type="II")
Anova Table (Type II tests)

Response: VO2
                Sum Sq   Df    F value       Pr(>F) 
Body.mass       962870    1     45.605   0.00003144 ***
Residuals       232245   11 
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Standard error of regression

S, the Residual Standard Error (aka Standard error of regression), is an overall measure to indicate the accuracy of the fitted line: it tells us how good the regression is in predicting the dependence of response variable on the independent variable. A large value for S indicates a poor fit. One equation for S is given by

In the above example, S = 145.3 (underlined, bold in regression output above). We can see how if SS_residual is large, S will be large indicating poor fit of the linear model to the data. However, by itself S is not of much value as a diagnostic as it is difficult to know what to make of 145.3, for example. Is this a large value for S? Is it small? We don’t have any context to judge S, so additional diagnostics have been developed.

Coefficient of determination

R², the coefficient of determination, is also used to describe model fit. R ², the square of the simple product moment correlation r, can take on values between 0 and 1 (0% to 100%). A good model fit has a high R ² value. In our example above, R ² = 0.8057 or 80.57%. One equation for R ² is given by

A value of R ² close to 1 means that the regression “explains” nearly all of the variation in the response variable, and would indicate the model is a good fit to the data. Note that the coefficient of determination, R ², is the squared value of r, the product moment correlation.

Adjusted R-squared

Before moving on we need to remark on the difference between R ² and adjusted R ². For Simple Linear Regression there is but one predictor variable, X; for multiple regression there can be many additional predictor variables. Without some correction, R ² will increase with each additional predictor variables. This doesn’t mean the model is more useful, however, and in particular, one cannot compare R ² between models with different numbers of predictors. Therefore, an adjustment is used so that the coefficient of determination remains a useful way to assess how reliable a model is and to permit comparisons of models. Thus, we have the Adjusted , which is calculated as

In our example above, Adjusted R ² = 0.3806 or 38.06%.

Which should you report? Adjusted R², because it is independent of the number of parameters in the model.

Both  and S are useful for regression diagnostics, a topic which we will discuss next (Chapter 17.8).

Questions

1. True or False. The simple linear regression is called a “best fit” line because it maximizes the squared deviations for the difference between observed and predicted Y values.
2. True or False. Residuals in regression analysis are best viewed as errors committed by the researcher. If the experiment was designed better, or if the instrument was properly calibrated, then residuals would be reduced. Explain your choice.
3. The USA is finishing the 2020 census as I write this note. As you know, the census is used to reapportion congress and also to determine the number of electoral college votes. In honor of the election for US President that’s just days away, in the next series of questions in this Chapter and subsequent sections of Chapter 17 and 18, I’ll ask you to conduct a regression analysis on the electoral college. For starters, make the regression of Electoral votes on 2010 census population. (Ignore for now the other columns, just focus on POP_2019 and Electoral.) Report the
   • regression coefficients (slope, intercept)
   • percent of the variation in electoral college votes explained by the regression (R²).
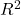4. Make a scatterplot and add the regression line to the plot

Data set

USA population year 2010 and year 2019 with Electoral College counts

Chapter 17 contents

• Introduction
• Simple Linear Regression
• Relationship between the slope and the correlation
• Estimation of linear regression coefficients
• OLS, RMA, and smoothing functions
• Testing regression coefficients
• ANCOVA – Analysis of covariance
• Regression model fit
• Assumptions and model diagnostics for Simple Linear Regression
• References and suggested readings (Ch17 & 18)