8 – Inferential statistics

Introduction

Statistical methods are important in biology because results of experiments are usually not clear-cut and therefore tests to support decisions between competing hypotheses are needed.

We will limit ourselves to a general discussion with examples, but beginning in this chapter, we start our introductions of specific types of statistical tests. As a reminder, our statistical philosophy is frequentist and follows the Null Hypothesis Significant Testing or NHST approach. Discussion of Bayesian statistical approaches are included as appropriate.

Thus, all statistical tests we will talk about share the following requirements or properties.

1. The type of data we have dictates which test or tests are appropriate.
2. We start with a clear description of the null hypotheses.
3. Set the Type I error rate, alpha (α). By convention, 5% is often used (Cowles and David 1982)
4. We must be aware of the assumptions our statistical tests make and what, if any, modifications to them we can make.
5. Correct computation of the test statistic and degrees of freedom.
6. Comparison of the critical value and the test statistic value, with interpretation and significance testing (p-value, Bayesian Factor, cf. discussion in Goodman 2008).

We can provide a flow-chart of these steps (Fig. 1).

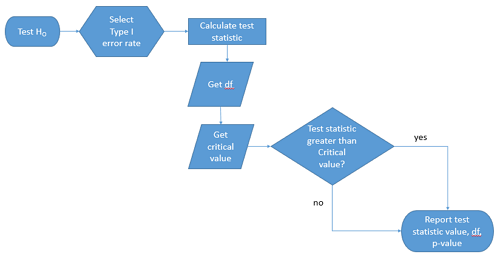
Figure 1. NHST decision flow chart

While we want to avoid the impression that statistical analysis is simply a matter of following a step-by-step protocol (Fig. 1), it nevertheless may be helpful to think of it as such, understanding all the while that there are caveats and assumptions that accompany the choices we make while following the protocol.

Chapter 8 contents

• Introduction
• The null and alternative hypotheses
• The controversy over proper hypothesis testing
• Sampling distribution and hypothesis testing
• Tails of a test
• One sample t-test
• Confidence limits for the estimate of population mean
• References and suggested readings