9.3 – Yates continuity correction

Introduction

Yates continuity correction: Most statistical textbooks at this point will note that critical values in their table (or any chi-square table for that matter) are approximate, but don’t say why. We’ll make the same directive — you may need to make a correction to the \chi^2 for low sample numbers. It’s not a secret, so here’s why.

We need to address a quirk of the \chi^2 test: the chi-square distribution is a continuous function (if you plotted it, all possible values between, say, 4 and 3 are possible). But the calculated \chi^2 statistics we get are discrete. In our HIV-HG co-infection problem from the previous subchapter, we got what appears to be an exact answer for P, but it is actually an approximation.

We’re really not evaluating our test statistic at the alpha levels we set out. This limitation of the goodness of fit statistic can be of some consequence — increases our chance to commit a Type I error — unless we make a slight correction for this discontinuity. The good news is that the \chi^2 does just fine for most df, but we do get concerned with it’s performance at df = 1 and for small samples.

Therefore, the advise is to use a correction if your calculated \chi^2 is close to the critical value for rejection/acceptance of the null hypothesis and you have only one df. Use the Yate’s continuity correction to standard \chi^2 calculation, \chi_{c} ^2.

    \begin{align*} \chi_{c} ^2 = \sum_{i = 1}^{k}\frac{\left (\left | O_{i} - E_{i} \right | - 0.5 \right )^2}{E_{i}} \end{align*}

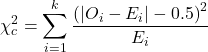
For the 2×2 table (Table 1), we can rewrite Yates correction

    \begin{align*} \chi_{c} ^2 =\frac{\left ( ad-bc \right )^{2}N}{\left( a+b\right )\left( c+d\right )\left( a+c\right )\left( b+d\right )} \end{align*}

Our concern is this: without the correction, Pearson’s \chi^2 test statistic will be biased (e.g., the test statistic will be larger than it “really” is), so we’ll end up rejecting the null hypothesis when we shouldn’t (that’s a Type I error). This becomes an issue for us when p-value is close to 5%, the nominal rejection level: what if p-value is 0.051? Or 0.049? How confident are we in concluding accept or reject null hypothesis, respectively?

I gave you three examples of goodness of fit and one contingency table example. You should be able to tell me which of these analyses it would be appropriate to apply to correction.

More about continuity corrections

Yates suggested his correction to Pearson’s \chi_{c} ^2 back in 1934. Unsurprisingly, new approaches have been suggested (e.g., discussion in Agresti 2001). For example, Nicola Serra (Serra 2018; Serra et al 2019) introduced

    \begin{align*} \chi_{Serra} ^2 =\frac{16}{N^{3}}\left ( ad-bc \right ) \end{align*}

Serra reported favorable performance when sample size was small and the expected value in any cell was 5 or less.

R code

When you submit a 2X2 table with one or more cells less than five, you could elect to use a Fisher exact test, briefly introduced here (see section 9.5 for additional development), or, you may apply the Yates correction. Here’s some code to make this work in R.

Let’s say the problem looks like Table 1.

Table 1. Example 2X2 table with one cell with low frequency.

Yes No
A 8 12
B 3 22

At the R prompt type the following

library(abind, pos=15)
#abind allows you to combine matrices into single arrays
.Table <- matrix(c(8,12,3,22), 2, 2, byrow=TRUE)
rownames(.Table) <- c('A', 'B')
colnames(.Table) <- c('Yes', 'No') # when you submit, R replies with the following table
.Table  # Counts
 Yes No
A  8 12
B  3 22

Here’s the \chi^2 command; the default is no Yates correction (i.e., correct=FALSE); to apply the Yates correction, set correct=TRUE

.Test <- chisq.test(.Table, correct=TRUE)

Output from R follows

.Test
    Pearson's Chi-squared test with Yates' continuity correction
data:  .Table
X-squared = 3.3224, df = 1, p-value = 0.06834

Compare without the Yates correction

.Test <- chisq.test(.Table, correct=FALSE)
.Test
    Pearson's Chi-squared test
data:  .Table
X-squared = 4.7166, df = 1, p-value = 0.02987

Note that we would reach different conclusions! If we ignored the potential bias of the un-corrected \chi^2 we would be tempted to reject the null hypothesis, when in fact, the better answer is not to reject because Yates-corrected p-value is greater than 5%.

Just to complete the work, what does the Fisher Exact test results look like (see section 9.5)?

fisher.test(.Table)
    Fisher's Exact Test for Count Data
data:  .Table
p-value = 0.04086
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.9130455 32.8057866
sample estimates:
odds ratio 
  4.708908

Which to use? The Fisher exact test is just that, an exact test of the hypothesis. All possible outcomes are evaluated and we interpret the results as likely as p=0.04086 if there is actually no association between the treatment (A vs B) and the outcome (Yes/No) (see section 9.5).

Questions

  1. With respect to interpreting results from a \chi^2 test for small samples, why use the Yates continuity correction?
  2. Try your hand at the following four contingency tables (a – d). Calculate the \chi^2 test, with and without the Yates correction. Make note of the p-value from each and note any trends.

(a)

Yes No
A 18 6
B 3 8

(b)

Yes No
A 10 12
B 3 14

(c)

Yes No
A 5 12
B 12 18

(d)

Yes No
A 8 12
B 3 3

3. Chapter 9.1, Question 1 provided an example of a count from a small bag of M&Ms. Apply the Yates correction to obtain a better estimate of p-value for the problem. The data were four blue, two brown, one green, three orange, four red, and two yellow candies.

  • Construct a table and compare p-values obtained with and without the Yates correction. Note any trend in p-value

Chapter 9 contents