4.1 – Bar (column) charts
Introduction
Bar chart, also called a bar graph, or column chart in many spreadsheet apps (e.g., Google Sheets, Microsoft Excel, Libreoffice Calc — “bar charts” is reserved for horizontal bar plots), are used to compare counts among two or more categories, i.e., an alternative to pie charts (Fig. 1).
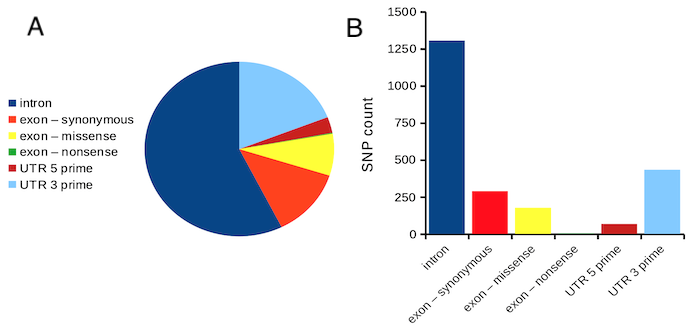
Figure 1. Single nucleotide variants for human gene ACTB by DNA and functional element (data collected 19 May 2022 from NCBI SNP database with Advanced search query). A. Pie chart. Note that slide for “exon – nonsense” is not visible. B. Bar chart – color coded bars to facilitate comparison with pie chart.
Although bar charts are common in the literature (Cumming et al 2007; Streit and Gehlenborg 2014), bar charts may not be a good choice for comparisons of ratio scale data (Streit and Gehlenbor 2014). Bar charts for ratio data are misleading. Parts of the range implied by the bar may never have been observed: the bars of the chart always start at zero. Box (whisker) plots are better for comparisons of ratio scale data and are presented in the next section of this chapter. That said, I will go ahead and present how to create bar chars for both count, generally considered acceptable, and ratio scale data, for which their use is controversial.
Purpose of the bar chart
Like all graphics, a bar chart should tell a story. The purpose of displaying data is to give your readers a quick impression of the general differences among two or more groups of the data. For counts, that’s where the bar chart comes in. The bar chart is preferred over the pie chart because differences are represented by lengths of the bars in the bar chart. Differences among categories in a pie chart are reflected by angles, and it seems that humans are much better at judging lengths than angles.
Bar chart with counts
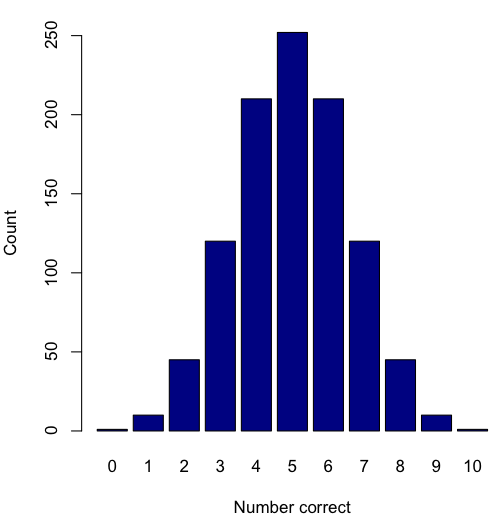
Figure 2. A simple bar chart
myCombo <- seq(0,10, by=1)
myCounts <- choose(10, myCombo) #combinations
barplot(myCounts, names.arg = myCombo, xlab = "Number correct", ylab = "Count",col = "darkblue")A stacked bar chart is used to
myCombo <- seq(0,10, by=1)
myCounts <- choose(10, myCombo) #combinations
barplot(myCounts, names.arg = myCombo, xlab = "Number correct", ylab = "Count",col = "darkblue")
Figure 3. The luxury ship RMS Titanic, which sunk 15 April 1912, More than 1500 souls were lost. Public domain image, Wikipedia. Click image to view full sized image.
Stacked bar chart, data set TitanicSurvival in package carData.
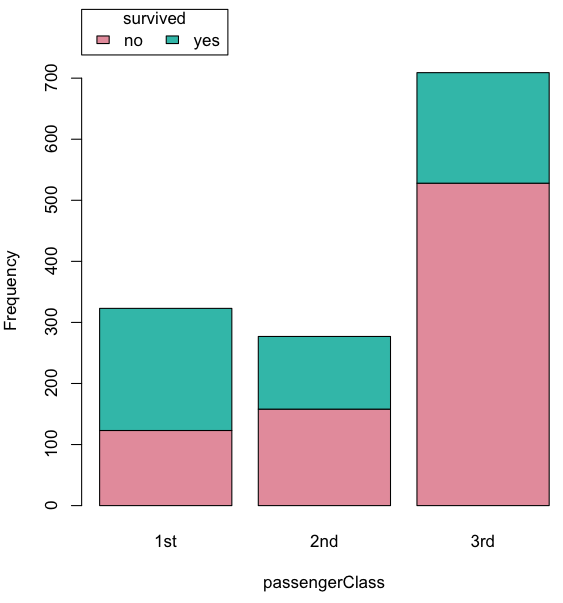
Figure 4. A stacked bar chart, survival Titanic
Barplot(passengerClass, by=survived, style="divided", legend.pos="above", xlab="passengerClass", ylab="Frequency")Bar charts with error bars
Although many data visualization specialists argue against the bar chart, their use is well established. For the familiar bar chart with ratio scale data, the X (horizontal) axis displays the categories of one variable (e.g., location, or treatment group). You plot groups to emphasize comparisons. The Y (vertical) axis then is the mean for each group.
You need error bars. If the mean is displayed, some measure of precision should be (must be?) displayed (Cumming et al 2007). And, as you should recall by now, your choices are standard deviation (Chapter 3.2), standard error of the mean (SEM) (Chapters 3.2, 3.4), or confidence interval (see Chapter 3.4). It is strongly advised, that without a representation of precision, one should not interpret trends or group differences from representations of means (i.e., height of bars) alone.
The bar charts on this page are means plus or minus the standard error of the mean, + SEM. We’ll discuss which choice to make.
Examples
The Copper_rats_PMID3357063 dataset will be used for the next series of graphs (Data set). Refer to Mike’s Workbook for Biostatistics Part07 to review how to import the data.
A portion of the data set is shown below
head(Copper)
Diet Body Heart Liver
1 Adequate-Cu 320.1381 1.125037 10.259657
2 Adequate-Cu 329.6879 1.158982 9.843295
3 Adequate-Cu 327.9838 1.090374 9.855975
4 Adequate-Cu 334.6669 1.118183 9.942997
5 Adequate-Cu 338.3134 1.172636 9.860971
6 Adequate-Cu 345.4608 1.056183 8.885820The data set consists of organ weights (heart, liver) from rats fed a diet adequate in copper, deficient in copper, and then a third group who received the adequate diet from perspective of amount of copper, but calorie restricted to match the decreased feeding rates of the rats fed the copper deficient diet. Copper is an essential trace element in our diet. The data set was simulated from descriptive statistics (means, standard deviation, number of subjects) of published data by sampling from a normal distribution. (Table 1, Ovecka et al 1988).
On we go with some graphs.
Note. R has many options to create bar charts, and especially ggplot2 can be used to great advantage, but there is a learning curve. One of the great things about R is that folks help each other by sharing code. For example, http://www.cookbook-r.com/Graphs/Plotting_means_and_error_bars_(ggplot2)/
But, I’m still learning about R graphics, and for bar charts with error bars, I find other packages more straight-forward. So, I’ll use this moment to point out that making a good graph is more about the end product then the particular tools. I have been using other tools for years to make my graphics, so I tend to default on these options first. Graphs presented here are mostly from Veusz software program (pronounced “views”). I like it because the software allows me to edit any of the elements of the graph.
Here’s a typical looking bar chart with ratio scale data: means ± SEM. Let’s look at them more critically.
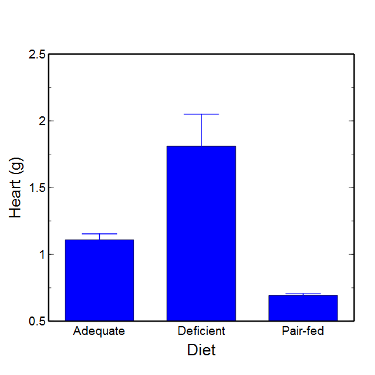
Figure 5. A bar chart with error bars (standard error of the mean).
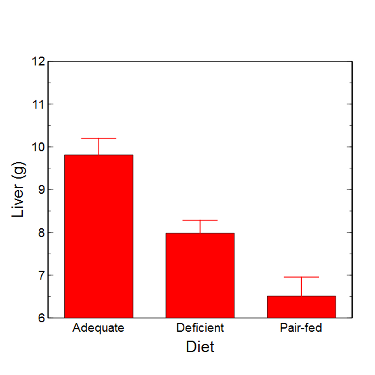
Figure 6. Another bar chart. with standard errors of mean
When making comparisons, make sure the axes have the same scale, or consider putting the graphs together.
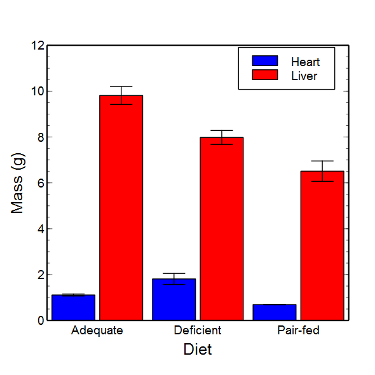
Figure 7. Bar chart that allows for a comparison among levels of a a factor (organs, liver vs. heart).
Analysis note: For variables that covary with body size (for example, on average, tall people generally are heavier too), is how to present (and analyze) the data in such a way that body size is accounted for. Here, the solution was to express organ weight as the ratio of organ weight to body weight for the mice. This may or may not be a good solution, and the answer is too complicated for us now (has to do with a thing called allometric scaling), but I wanted to at least present the issue and show how the graphics can be improved to handle some of these concerns.
Here’s the organ weights again, but taken as ratio of body mass.
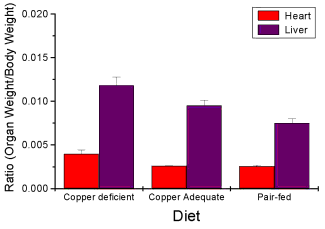
Figure 8. Same chart as in Figure 6, but on ratios.
Note 2. Lets be clear about expectations of you for statistics class. Now, R (and Rcmdr) do lots of graphics, pretty much anything you want, but it is not as friendly as it could be. For BI311 homework, the default graphics available via Rcmdr will generally be adequate for assignments. R and Rcmdr has many bar chart options, but there isn’t a straightforward way to get the error bars, unless you are willing to enter some code to the command line or learn a particular package (like gplots or ggplot2).
How to make a bar chart with error bars in R
Option 1. First, let’s try a work-around. Instead of an error bar option for bar chart menu, Rcmdr provides a plot of means that allows you to plot with error bars. These are equivalent graphs, the “bar chart” and the “plot of means”, though you should favor the bar chart format for publishing.
Rcmdr: Graphs → Plot of means…
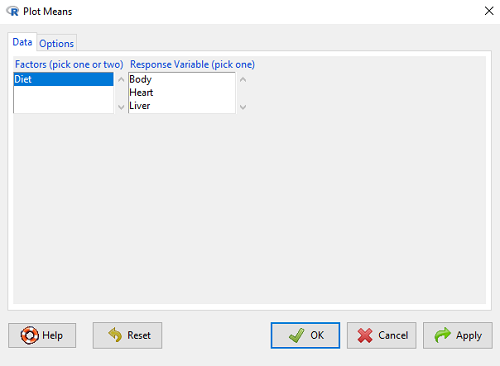
Figure 9. Rcmdr menu popup for Plots Means
Here, Rcmdr takes the data and calculates the mean and your choice of standard errors or deviations, confidence intervals, or no error bars. the resulting graph is below.
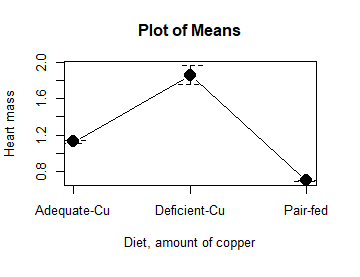
Figure 10. Plot of means
That’s an ugly graph (Fig. 10). Functional, good enough for data exploration and preliminary results, and certainly good enough for a Biostatistics homework or report. Additionally, connecting the dots here is a no-no. It implies that if we had measured categories between “adequate copper” and “deficient copper,” then the points would fall on those lines. That would be a complete guess. So, why did I include the connecting lines? That was the default setting for the command, and it makes the point — think before you click. One argument for connecting points in a graph is that it makes it easier for the reader to visualize trends.
This graph (Fig. 10) is fine for exploring data, but you will want to do better for publication.
Let’s make some better graphs with R
Once you are ready to go beyond the default settings available in Rcmdr, there is tremendous functionality in R for graphics. To access R’s potential, you’ll need to get into the commands a bit. I’m going to continue to try and shield you from the programming aspects of R, but from time to time you really need to see what is possible with R. Graphics is one such area. I use the package gplots, with 23 different graphing functions (type at R prompt ?gplots to call up the manual pages).
gplots should be among the packages on your R installation; if not, then install the package and run library(gplots) to complete the installation. We’ll try the barchart2 function.
But first, we need to get means for each of our groups.
At the R command prompt:
hrtWt <- tapply(Dataset$HeartWt, list(Group=Dataset$Group), mean, na.rm=TRUE) This code extracts means from our HeartWt variable for each Group, then stores the three (in this case, because our data set has 3 groups) in the place holder I had called hrtWt. To verify that the three means are there, type “hrtWt” without the quotes then enter.
You should see
hrtWt Group Cu adequate Cu deficient Pair-fed
1.200000 1.566667 0.900000R functions used: tapply, list, mean; na.rm was not needed but would be used to remove all missing values (recall during our import phase we were asked how missing observations were noted in our file; the default is NA).
Next, I want to apply standard error bars
stdDEV <- tapply(Dataset$HeartWt, list(Group=Dataset$Group), sd, na.rm=TRUE)
cil <- hrtWt-(stdDEV/sqrt(3))
ciu <- hrtWt+(stdDEV/sqrt(3))I used cil and ciu to designate the lower cil and upper ciu values for my ± SEM (standard error of the mean). ciu stands for “confidence interval lower;” ciu stands for “confidence interval upper.”
Finally, here’s the plot command
barplot2(hrtWt, beside = TRUE, main=c("Mice fed different amounts of copper in diet"), col = c("blue", "red", "green"), xlab="Copper in diet", ylab="Heart mass (g)", ylim = c(0, 2), plot.ci=TRUE, ci.l=cil, ci.u=ciu)Now, draw a box around the graphic
box()Whew!
What does your new graph look like? My graph is below (Fig. 11).
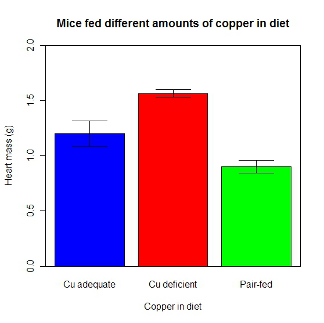
Figure 11. A bar chart using barplot2.
This works and the point is that once the script is written it easy to make small changes as you need in the future to make nice graphs.
If you are impatient like me, I like a GUI option, at least to start crafting the graph. The Rcmdr plugin KMggplot2 provides a good set of tools to make bar charts with error bars. An even better option I think is to use a software package that is designed for graphics, at least simple graphics like a bar chart. I use SciDAVis and Veusz for simple graphs like pie charts and bar charts; much easier to control.
ggplot2 bar charts with error bars
Nevertheless, here’s how to make a bar chart with error bars using ggplot2 (Fig. 11). First, we need to create a statistics summary. The script printed here was modified from scripts at R Graph Cookbook website.
require(plyr)
summarySE <- function(data=NULL, measurevar, groupvars=NULL, na.rm=FALSE,
conf.interval=.95, .drop=TRUE) {
length2 <- function (x, na.rm=FALSE) {
if (na.rm) sum(!is.na(x))
else length(x)
}
#returns a vector with N, mean, and sd
datac <- ddply(data,groupvars, .drop=.drop,
.fun = function(xx,col){
c(N=length2(xx[[col]],na.rm=na.rm),
mean=mean(xx[[col]],na.rm=na.rm),
sd=sd(xx[[col]],na.rm=na.rm)
)
},
measurevar
)
#Rename the "mean" column
datac <- rename(datac,c("mean"=measurevar))
#Calculate the standard error of the mean
datac$se <- datac$sd/sqrt(datac$N)
#Get confidence interval
ciMult <- qt(conf.interval/2 + .5, datac$N-1)
datac$ci <- datac$se*ciMult
return(datac)
}Applying this function to the BMI dataset yields the following output.
sumBMI <- summarySE(BMI, measurevar="BMI", groupvars=c("Sex", "Smoke"));sumBMI
Sex Smoke N BMI sd se ci
1 F No 23 26.83567 7.610271 1.5868511 3.290928
2 F Yes 14 25.76133 4.658625 1.2450698 2.689810
3 M No 10 26.35731 3.363575 1.0636557 2.406156
4 M Yes 27 26.71879 4.675631 0.8998256 1.849618Now we are ready to make the bar chart with error bars
ggplot(tgc,aes(x=Smoke,y=BMI,fill=Sex)) +
geom_bar(position=position_dodge(),stat="identity",color="black") +
geom_errorbar(aes(ymin=BMI,ymax=BMI+se),width=.2,position=position_dodge(.9))
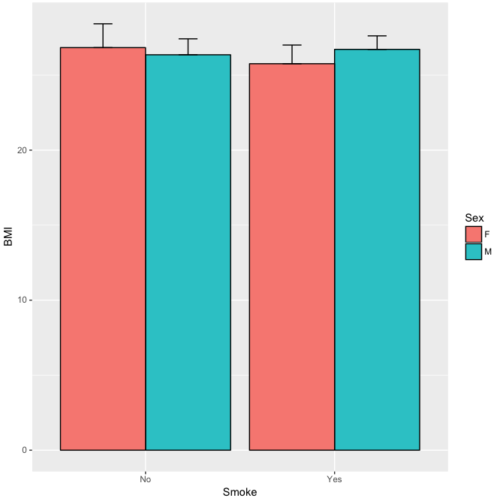
Figure 12. A barchart from ggplot2
Questions
1. Why should you use box plots and not bar charts to display comparisons for a ratio scale variable between categories? Obtain a copy of the article by Streit and Gehlenbor 2014 — it’s free! After reading, summarize the pro and cons for box plots over bar charts with error bars.
2. Enter the following data into R. The data are sulfate levels in water, parts per million.
type = c("Palolo Stream","Chaminade tap water", "Aquafina","Dasani")
sulfateppm =c(11, 14, 5, 12)
try = data.frame(type,sulfateppm)
byWater = tapply(try$sulfateppm,list(Group=try$type),mean)Make a simple bar chart using the boxplot2 function in gplots package.
3. Change the range of values on the vertical axis to 0, 20
4. Change the color of the bars from gray to blue
5. Add a label to the vertical axis, “Sulfates, ppm” (without the quotes)
6. Add a box around the graph.
Data set
| Diet | Body | Heart | Liver |
|---|---|---|---|
| Adequate-Cu | 320.1381 | 1.125037 | 10.259657 |
| Adequate-Cu | 329.6879 | 1.158982 | 9.843295 |
| Adequate-Cu | 327.9838 | 1.090374 | 9.855975 |
| Adequate-Cu | 334.6669 | 1.118183 | 9.942997 |
| Adequate-Cu | 338.3134 | 1.172636 | 9.860971 |
| Adequate-Cu | 345.4608 | 1.056183 | 8.88582 |
| Adequate-Cu | 343.089 | 1.081261 | 10.166647 |
| Adequate-Cu | 328.3403 | 1.111278 | 10.124185 |
| Adequate-Cu | 324.9723 | 1.189194 | 10.158402 |
| Adequate-Cu | 325.2378 | 1.14715 | 9.939521 |
| Deficient-Cu | 195.5052 | 1.90973 | 7.907565 |
| Deficient-Cu | 182.7809 | 1.823672 | 8.430167 |
| Deficient-Cu | 184.3701 | 1.632249 | 7.619104 |
| Deficient-Cu | 193.7867 | 1.831765 | 8.742489 |
| Deficient-Cu | 180.0417 | 1.710367 | 7.975879 |
| Deficient-Cu | 208.5349 | 2.495623 | 8.652445 |
| Deficient-Cu | 182.3048 | 1.262053 | 7.257726 |
| Deficient-Cu | 203.0413 | 2.153639 | 8.081782 |
| Deficient-Cu | 193.3829 | 1.986028 | 7.807328 |
| Deficient-Cu | 195.0523 | 1.76975 | 8.297611 |
| Pair-fed | 211.0858 | 0.6911343 | 6.251177 |
| Pair-fed | 210.4041 | 0.6928067 | 7.696669 |
| Pair-fed | 208.5969 | 0.6911901 | 6.973803 |
| Pair-fed | 209.3333 | 0.7039211 | 6.629303 |
| Pair-fed | 208.8889 | 0.7077486 | 6.038704 |
| Pair-fed | 208.2994 | 0.7004535 | 6.606877 |
| Pair-fed | 209.4524 | 0.6915543 | 6.228888 |
| Pair-fed | 210.2699 | 0.6984497 | 6.638466 |
| Pair-fed | 208.8142 | 0.7214847 | 6.353705 |
| Pair-fed | 209.2977 | 0.6848656 | 6.536642 |