16.3 – Data aggregation and correlation
Introduction
Correlations are easy to calculate, but interpretation beyond a strict statistical interpretation, e.g., two variables linearly associated, may be complicated — caution is recommended. With respect to interpreting a correlation, caution and temperance is warranted. As previously discussed, “correlation is not causation,” is well known, but identifying when this applies to a particular analysis is not straight-forward. We introduced the problem of two variables sharing a hidden covariation which drives the correlation. In this section we introduce how correlations among grouped (aggregated) data may be quite different from the underlining individual correlations (cf. Robertson 1950, Greenland 2001, Portnov et. al 2006).
Perfect (+1 or -1) correlation?
What if an estimated correlation value between two ratio scale variables turns out to be +1 or -1, the limits of the possible range of the correlation coefficient? Trivially, the reported value of one for the coefficient may be the result of rounding, it was actually 0.97. But, for argument’s sake, let’s assume the coefficient value was 1.0 to as many significant figures as the calculator may report. Another trivial possibility: suspect you’re looking at a case for which the two variables are the same thing, but on different scale. For example, the correlation between a range of temperatures measured in degrees Fahrenheit and then converted to degrees Celsius trivially will be +1.
Less trivially, a correlation of +1 or -1 may reveal that two variables are simply restatements of the same measured variable. Additionally, perfect correlation may reflect construction of a composite variable. Composite variables are examples of indexes, and are constructed from related variables by the researcher in order to better predict multivariate outcomes (see also Latent variables). Refs to add Diamantopoulos and Winklhofer 2001; Bollen and Diamantopoulos 2015
Data aggregation
Data aggregation or grouping refers to processes to group data in a summary form. Considerable public health data is presented this way. For example, CDC reports table after table of data about morbidity and mortality of United States of America population. Data are grouped by age, cities, counties, ethnicities, gender, and states and reports are generated to convey the status of health peoples. Similarly, education statistics, economic statistics, and statistics about crime are commonly crafted from grouped data of what originally was data for individuals.
Correlations between groups may yield spurious conclusions
Researchers interested in testing hypotheses like BMI is correlated with mortality (Flegal et al 2013, Kltasky et al 2017), or health disparities and ethnicity (Portnov et. al 2006), may use grouped data. In 16.2 we introduced the concept of spurious correlation. Correlations between grouped data may also mislead.
Consider the hypothesis that religiosity may deter criminal behavior. This hypothesis has been tested many times dating back to at least the 1940s (reviewed in Salvatore and Rubin 2018). Conclusions about religious beliefs range from negative association with criminal behavior to, in some reports, holding religious beliefs makes one more likely to commit crime. Testing versions of the hypothesis — what causes criminality in some individuals — among a variety of putative causal agents pops up through the history of biology research, arguably beginning with Galton. I hope you appreciate how challenging this would be to actually resolve — defining criminal behavior itself is laden with all kinds of sociology traps — and for a biologist, reeks of eugenics lore (Horgan 1993).
that all said, let’s proceed to test the religion-criminality hypothesis with aggregated data. The null hypothesis would be no association between crime statistics and numbers of churches. We can also ask about association between crime and non-religious or secular beliefs. I added numbers of Catholic churches and secular humanists groups for cities larger than 100K population by Internet search (FBI for crime statistics, Wikipedia for cities). Figure 1 and Figure 2 report crimes statistics aggregated by cities in the United States and by number of Catholic churches (Fig. 1), and by number of secular humanists groups (Fig. 2) in the same cities.
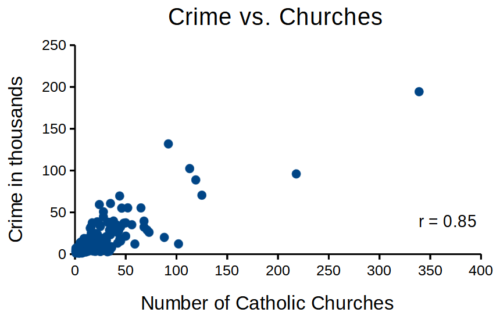
Figure 1. Scatterplot crime rates of cities by number of Catholic churches
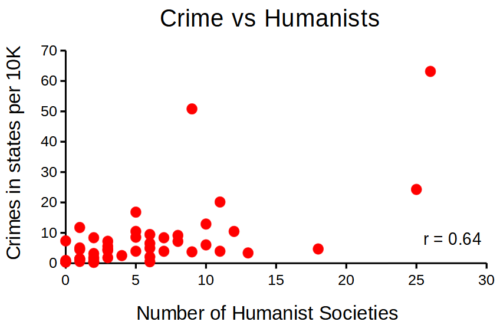
Figure 2. scatterplot crime rates of cities by number of secular humanist associations.
We’ll just take the numbers on faith (of course, we should think about the bunching around the origin — do we really think Internet search will get all of the secular groups, for example? Or is it really the case that several cities have no secular groups?). Both correlations were statistically different from zero, crime by churches (P < 0.001) and crime by secular groups (P < 0.001).
Now, having read Chapter 16.2 I trust you recognize immediately that there’s an important hidden covariate in common. Cities with small populations will have small numbers of crimes reported and smaller numbers of churches compared to large cities. Indeed, the correlation between population and crime for these cities was 0.89 and 0.97, respectively. However, after estimating the partial-correlations, we still have some explaining to do. For crime and churches, the partial correlation was +0.37 (p-value = 0.009); for crime and secular humanist groups, the partial correlation was -0.37 (p = 0.018). These results suggest that persons are more likely to commit crimes in cities with lots of Catholic churches whereas criminal behavior by individuals is less likely where secular humanist groups are numerous.
Before we start pointing fingers, the analysis presented here is a classic ecological fallacy. By grouping the data we lose information about the individuals, and it is the individuals to which the hypothesis applied. Thus, we are at risk of making incorrect conclusions by assuming that the individual is characterized by the group. The hypothesis remains challenging to test (how does one get a valid assessment of an individual’s religiosity? The hypothesis is challenging to test, but studies of individuals tend to find no association or a negative association between criminal behavior and religiosity (Salvatore and Rubin 2018). Crime statistics may underestimate criminal behavior, e.g., embezzlement and other “white” crime), but a proper study would look to survey of individuals (Fig. 3).
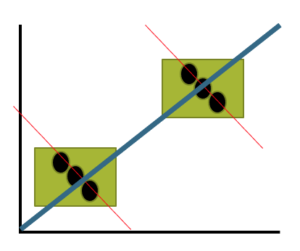
Figure 3. Illustration of ecological fallacy: positive association at level of groups (boxes, solid blue line), but negative association at level of individuals (black circles, red dashed lines).
Studies that use aggregate data test hypotheses about the groups, not about individuals in the groups. These studies are appropriate for comparing groups, e.g., health disparities by ethnicity (Wang Kong et al 2022) or gender (Read and Gorman 2010; Cooper et al 2023), or comparisons among counties (e.g., urban vs. rural) for medical resources (Anderson and Zimmerman 2024), or other “social determinates of health” (Crawfolrd 1977; Braveman and Gottlieb 2014), but one cannot conclude that the association is present for members of the group.
Bubble charts
Given we know about the covariation with population size, is there a better way to visualize the crime by number of churches and crime by number of humanist societies? One option is the bubble chart.
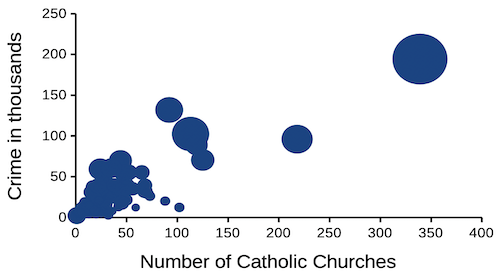
Figure 4. Bubble plot of data used to make Figure 1. Plot by LibreOffice Calc.
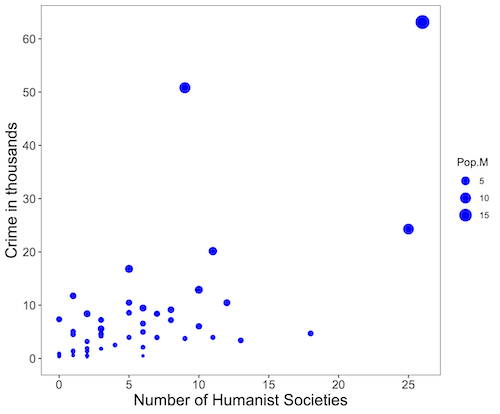
Figure 5, Bubble plot of data used to make Figure 2. Plot by ggplot2 package in R.
R code for Figure 5.
# STDHA site by Dr A. Kassambara https://www.sthda.com/english/
myPlot <- ggplot(humanists, aes(x = Humanist, y = Crime.K, size = Pop.M)) +
geom_point(color="blue", aes(size = Pop.M)) + theme_bw() + ylab("Crime in thousands") +
xlab("Number of Humanist Societies")
myPlot2 <- myPlot + theme(axis.title=element_text(size=16),
axis.text.x=element_text(size=12), axis.text.y=element_text(size=12),
panel.grid.major = element_blank(), panel.grid.minor = element_blank())
myPlot2 + scale_x_continuous(breaks=seq(0,30,5)) +
scale_y_continuous(breaks=seq(0,65,10))
Questions
1. What’s the most likely statistical explanation for why there is an apparent correlation between rates of autism and childhood vaccination rates? See Davidson 2017.
2. For the following data set, calculate the Pearson product moment correlation and, separately, the Spearman rank correlation. Report the values of the coefficients and provide an interpretation of the results.
v1: 68, 72, 68, 69, 65, 76, 58, 62, 69, 67, 66, 71, 70
v2: 1.727, 1.829, 1.727, 1.753, 1.651, 1.93, 1.473, 1.575, 1.753, 1.702, 1.676, 1.803, 1.778
3. For a small data set on human males ages 24 to 59, the estimated correlation between weight and the calculated BMI index was 0.68. (BMI is an example of a composite variable.) Explain why the correlation between weight and BMI is not +1.