Distribution tables
Tables of common probability distributions
Interpolating p-values
Tables of common probability distributions
The appendix provides critical values and probabilities for a few of the most common probability distributions. The tables were generated by appropriate functions in R. Code is provides with each statistical table
Table of Z of standard normal probabilities
Table of Chi-square critical values
Table of Critical values of Student’s t-distribution
Table of Critical values of F-distribution
Interpolating p-values
We have a calculated test statistic of 3.333 from a chi-square test; How likely is our test statistic value of 3.333 and the null hypothesis was true? (Remember, “true” in this case is a shorthand for our data was sampled from a population in which the Hardy-Weinberg expectations hold for example). When I check the table of critical values of the chi-square test for the “exact” P-value, I find that our test statistic value falls between a P-value 0.10 and 0.05 (represented in the table below). How can I find our exact P-value, u (unknown)?
| statistic | p-value |
| 3.841 | 0.05 |
| 3.333 | u |
| 2.706 | 0.10 |
Short answer, use R. In the case of We can interpolate to find u. If we assume the change in probability between 2.706 and 3.841 for the chi-square distribution is linear (it’s not, but it’s close), then we can do so simple interpolation.
We set up what we know on the right hand side equal to what we don’t know on the left hand side of the equation,
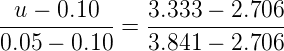
and solve for u. Then, u is equal to
R function pchisq() gives a value of P = 0.0679. Our interpolated value is close, but not the same. Of course, you should go with the result from R; we mention how to get the approximate p-value by interpolation for completeness, and, in some rare instances, you might need to make the calculation.