14.7 – Rcmdr Multiway ANOVA
Introduction
We have been talking about the two-way randomized, balanced, replicated design. Here, we take you step by step through use of R to conduct the multiway ANOVA.
R code: Multiway ANOVA
Rcmdr: Statistics → Means → Multiway ANOVA… we will review this as Option 1
or
Rcmdr: Statistics → Fit Models → Linear model… we will review this as Option 2
In either case, as a reminder, your data set must be stacked worksheet, like the data in this worksheet
Table 1. Data set, example.14.7†
| Diet | Population | Response |
| A | 1 | 4 |
| A | 1 | 6 |
| A | 1 | 5 |
| A | 2 | 5 |
| A | 2 | 8 |
| A | 2 | 9 |
| B | 1 | 12 |
| B | 1 | 15 |
| B | 1 | 11 |
| B | 2 | 5 |
| B | 2 | 7 |
| B | 2 | 8 |
Option 1
Your first option is to use the ANOVA menus via “Means.” This is a perfectly good way to handle a standard two-way, fully-crossed, fixed effects model. However, other designs will not run with this command and R will return a report of errors for ANOVA models that do not conform to the replicated, balanced, crossed design.
Rcmdr: Statistics → Means → Multiway Analysis of variance …
Factors: highlight “Diet” AND “Population”
Response variable: pick one (in this window, all we see is “Response”)
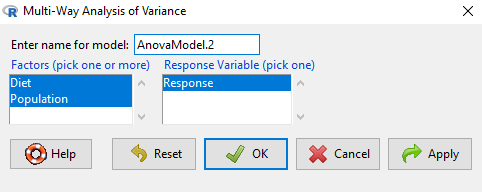
Figure 1. Screenshot Rcmdr multi-way ANOVA.
†Note: Don’t forget to convert numeric Population to factor
Interpret the output
AnovaModel.2 <- (lm(Response ~ Diet*Population, data=example.14.7))
Anova(AnovaModel.2)
Anova Table (Type II tests)
Response: Response
Sum Sq Df F value Pr(>F)
Diet 36.750 1 12.2500 0.008079 **
Population 10.083 1 3.3611 0.104104
Diet:Population 52.083 1 17.3611 0.003136 **
Residuals 24.000 8
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
tapply(example.14.7 Response, list(Diet=example.14.7 Diet,
+ Population=example.14.7 Population), mean, na.rm=TRUE) # means
Population
Diet 1 2
A 5.00000 7.333333
B 12.66667 6.666667
tapply(example.14.7 Response, list(Diet=example.14.7 Diet,
+ Population=example.14.7 Population), sd, na.rm=TRUE) # std. deviations
Population
Diet 1 2
A 1.000000 2.081666
B 2.081666 1.527525
tapply(example.14.7 Response, list(Diet=example.14.71 Diet,
+ Population=example.14.7 Population), function(x) sum(!is.na(x))) # counts
Population
Diet 1 2
A 3 3
B 3 3
End R output
Summary of multi-way ANOVA command
The multi-way ANOVA command returns our ANOVA table plus the adjusted means, along with standard deviations and number of observations (counts). The adjusted means would then be good to put into a chart to present group comparisons following adjustments from the effects of levels within groups.
Rcmdr: Models → Graphs → Predictor effect plots …
Here’s the chart (hint: ![]() )
)
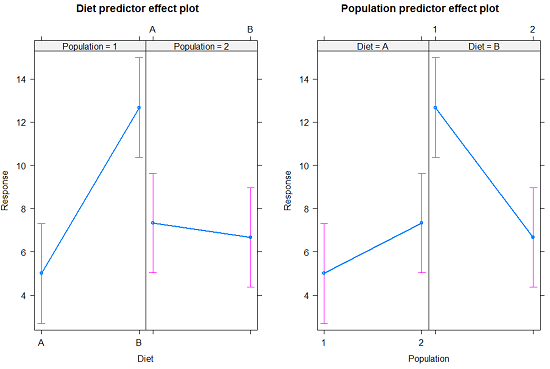
Figure 2. Predictor effect plots, Diet and Population on Response variable.
Option 2
A more general approach is to use the General linear model. This approach can handle the standard 2-way fixed effects ANOVA (above), but any other model as well. The model is Response ~ Diet*Population.
Rcmdr: Statistics → Fit Models → Linear model…
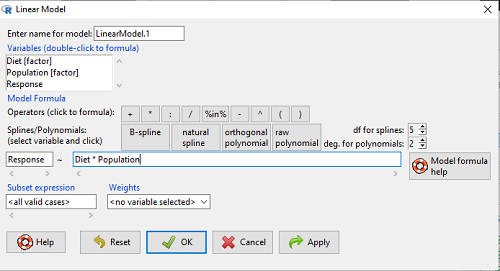
Figure 3. Screenshot Rcmdr linear model menu.
Interpret the output
LinearModel.1 <- lm(Response ~ Diet * Population, data=example.14.7)
summary(LinearModel.1)
Call:
lm(formula = Response ~ Diet * Population, data = example.14.7)
Residuals:
Min 1Q Median 3Q Max
-2.3333 -1.1667 0.1667 1.0833 2.3333
Coefficients:
Estimate Std. Error ..t value . Pr(>|t|)
(Intercept) . 5.000 1.000 . 5.000 .0.00105 **
Diet[T.B] . 7.667 ..1.414 . 5.421 .0.00063 ***
Population[T.2] .2.333 ..1.414 . 1.650 .0.13757
Diet[T.B]:Population[T.2] -8.333 ..2.000 -4.167 .0.00314 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.732 on 8 degrees of freedom
Multiple R-squared: 0.8047, Adjusted R-squared: 0.7315
F-statistic: 10.99 on 3 and 8 DF, p-value: 0.003285
End R output
Lots to sort through, so let’s begin with what is in common between the two approaches in Rcmdr, the Multi-way ANOVA command versus the linear model command.
Compare the two outputs
As a direct output, the linear model option does not provide an ANOVA summary table. Instead of our ANOVA table the linear model returns estimates of coefficients along with t-test results for each coefficient of the model from the lm() command output
Recall that we can get ANOVA tables through the following R commands via Rcmdr.
Rcmdr: Models → Hypothesis tests → ANOVA Table.
Lets do so for this linear model (accept the default for type of tests = “Type II”).
And the output is
Anova(LinearModel.1, type="II") Anova Table (Type II tests) Response: Response Sum Sq Df F value Pr(>F) Diet 36.750 1 12.2500 0.008079 ** Population 10.083 1 3.3611 0.104104 Diet:Population 52.083 1 17.3611 0.003136 ** Residuals 24.000 8 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
End R output
Now, were in business, and, using the lm() function, we have the estimates for each model coefficient plus our ANOVA table.
Same answer! Of course. Which to choose, Option 1 or Option 2? Use the lm() options; more flexible, covers more designs than the multiway ANOVA which is strictly for the crossed fully replicated design.
Questions
- Write out the two-way model described for the data in Table 1.
- Write the null hypotheses and provide a summary of the statistical significance of the model.