20.6 – Dimensional analysis

Introduction

This chapter is just a sampling of the many techniques for “reducing the dimensions” of a data set that contains many variables, aka high-dimensional space without eliminating the information contained among the many variables. The logic is similar to our discussions about model building — we may seek simple models at least in part so that we can see the big picture, not just each tree in an unhealthy forest.

Approaches can be categorized as feature extraction — a processing step to identify key characteristics contained in the larger data set into fewer, now transformed variables — or feature selection — the selection of a subset of the variables from among the full list which, presumably, contain redundant information. Cluster analysis and Principle Component Analysis are examples of feature extraction approaches. Stepwise regression, discussed in Ch18.5, is an example of a feature selection approach.

Principal component analysis

High dimensional data are reduced by linear transformation to sets of new vectors or coordinates. Each subsequent vector is orthogonal to the one proceeding it. The first component contains the largest amount of variation shared along the first linear adjustment, the second component contains the next largest amount of variation, and so on.

We demonstrate utility of PCA with Bumpus data from MorphoFun/psa, variable names changed.

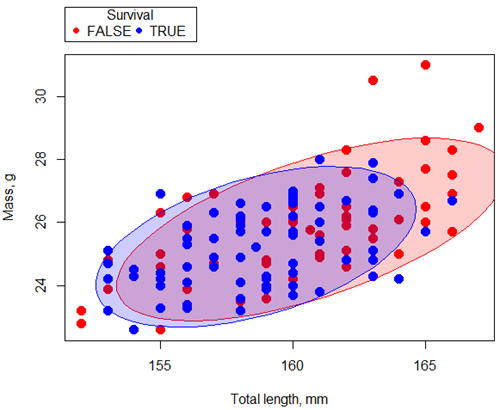
Figure 1. Scatterplot English swallow mass (g) by total length (mm) by survival following winter storm

R code for graph

car::scatterplot(Weight~Total_length | Survival, regLine=FALSE, smooth=FALSE, boxplots=FALSE,
ellipse=list(levels=c(.9)), by.groups=TRUE, grid=FALSE, pch=c(19,19), cex=1.5, col=c("red","blue"), xlab="Total length, mm", ylab="Mass, g", data=Bumpus)

Data ellipse — 90% of the pairwise points (red, did not survive; blue, did survive), not a confidence ellipse

Bumpus measured several traits, we want to use all of the data. However, highly correlated (Fig 2) and therefore multicollinear. Manly (1986) and others (see Vieira 2012) have applied PCA to this data set.

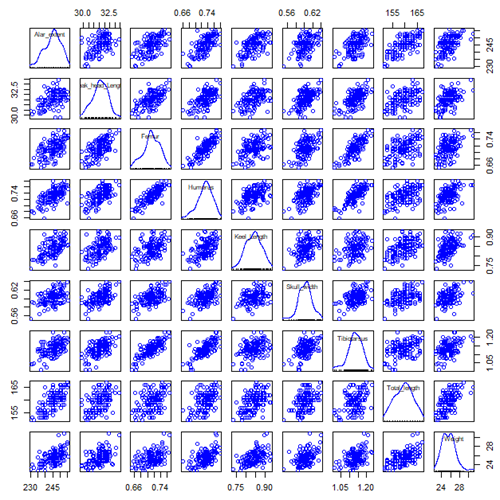
Figure 2. Scatterplot matrix of Bumpus English sparrow traits. Traits were (left-right): Alar extent (mm), length (tip of beak to tip of tail), length of head (mm), length of femur (in.), length of humerus (in.), length of sternum (in.), skull width (in.), length of tibio-taurus (in.), and weight (g)

R code for graph

car::scatterplotMatrix(~Alar_extent+Beak_head_Length+Femur+Humerus+Keel_Length+Skull_width+Tibiotarsus+Total_length+Weight, regLine=FALSE, smooth=FALSE, diagonal=list(method="density"), data=Bumpus)

Note 1: In Chapter 4, we discussed importance of white space and Y-scale for graphs that make comparisons. Figure 2 is a good example of where we trade-off the need for white space and concerns about telling the story — the various traits are positively correlated — against the dictum of an equal Y-scale for true comparisons.

R packages

factoextra

psa package from MorphoFun/psa/

Rcmdr: Statistics > Dimensional analysis > Principal component analysis …

.PC <-
princomp(~Alar_extent+Beak_head_Length+Femur+Humerus+Keel_Length+Skull_width+Tibiotarsus+Total_length+Weight, cor=TRUE, data=Bumpus)
cat("\nComponent loadings:\n")
print(unclass(loadings(.PC)))
cat("\nComponent variances:\n")
print(.PC\$sd^2)
cat("\n")
print(summary(.PC))
screeplot(.PC)
Bumpus <<- within(Bumpus, {
PC2 <- .PC\$scores[,2]
PC1 <- .PC\$scores[,1]
})
})

Importance of components

                              Comp.1     Comp.2
Standard deviation         2.3046882  0.9988978
Proportion of Variance     0.5901764  0.1108663
Cumulative Proportion      0.5901764  0.7010427

Cluster analysis

Cluster analysis or clustering is a multivariate analysis technique that includes a number of different algorithms for grouping objects in such a way that objects in the same group (called a cluster) are more similar to each other than they are to objects in other groups. A number of approaches have been taken, but loosely can be grouped into distance clustering methods (see Chapter 16.6 – Similarity and Distance) and linkage clustering methods: Distance methods involve calculating the distance (or similarity) between two points and whereas linkage methods involve calculating distances among the clusters. Single linkage involves calculating the distance among all pairwise comparisons between two clusters, then

Results from cluster analyses are often displayed as dendrograms. Clustering methods include a number of different algorithms hierarchical clustering: single-linkage clustering; complete linkage clustering; average linkage clustering (UPGMA) centroid based clustering: k-means clustering.

Cluster analysis is common to molecular biology and phylogeny construction and more generally is an approach in use for exploratory data mining. Unsupervised machine learning (see 20.14 – Binary classification) used to classify, for example, methylation status of normal and diseased tissues from arrays (Clifford et al 2011).

K-means clustering

Number of clusters

Iterations

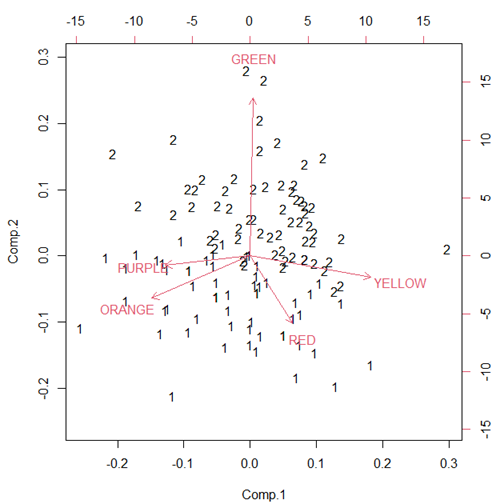
kmeans cluster bi-plot Skittles data set

Figure 3. Bi-plot of clusters, Skittles mini bags.

Hierarchical clustering

Ward’s method

Complete linkage

McQuitty’s method

Centroid linkage

A common way to depict the results of a cluster analysis is to construct a dendogram.

Questions

[pending]

References and further reading

Bumpus, H. C. (1898). Eleventh lecture. The elimination of the unfit as illustrated by the introduced sparrow, Passer domesticus. (A fourth contribution to the study of variation.). Biology Lectures: Woods Hole Marine Biological Laboratory, 209–255.

Clifford, H., Wessely, F., Pendurthi, S., & Emes, R. D. (2011). Comparison of clustering methods for investigation of genome-wide methylation array data. Frontiers in genetics, 2, 88.

Ferreira, L., & Hitchcock, D. B. (2009). A comparison of hierarchical methods for clustering functional data. Communications in Statistics-Simulation and Computation, 38(9), 1925-1949.

Fraley C, Raftery AE. (2002) Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc. 2002; 97(458):611–31.

Vieira, V. M. N. C. S. (2012). Permutation tests to estimate significances on Principal Components Analysis. Computational Ecology and Software, 2.

 

Chapter 20 contents

/MD